
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





3.7:
a: =>9x=225
=>x=25
b: =>4x^2=64
=>x^2=16
=>x=4 hoặc x=-4
c; =>4(x+1)=8
=>x+1=2
=>x=1
d: =>9(2-3x)^2=36
=>(3x-2)^2=4
=>3x-2=4 hoặc 3x-2=-4
=>x=2 hoặc x=-2/3
e: =>\(\sqrt{x-2}\left(\sqrt{x+2}-2\right)=0\)
=>x-2=0 hoặc x+2=4
=>x=2

Ta có \(\widehat{ACB}=38^0\) (so le trong)
\(AB=25+1,6=26,6\left(m\right)\)
\(\Rightarrow BC=\dfrac{AB}{tan\widehat{ACB}}=\dfrac{26,6}{tan38^0}\approx34\left(m\right)\)

Gọi vận tốc thực là x
Theo đề, ta có: \(\dfrac{54}{x+3}+\dfrac{54}{x-3}=7.5\)
=>\(\dfrac{54x-162+54x+162}{x^2-9}=7.5\)
=>7,5(x^2-9)=108x
=>7,5x^2-108x-67,5=0
=>x=15

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)




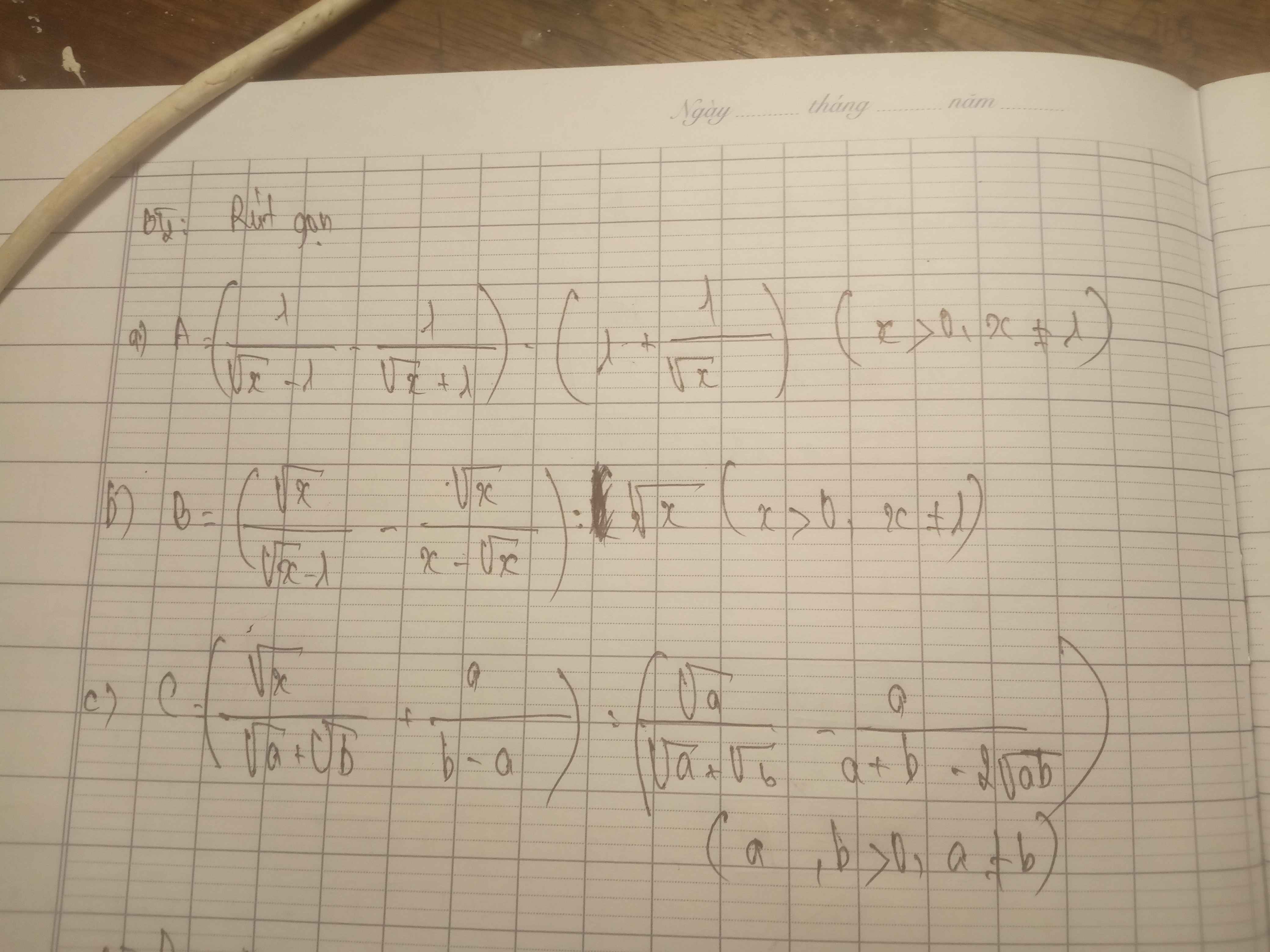
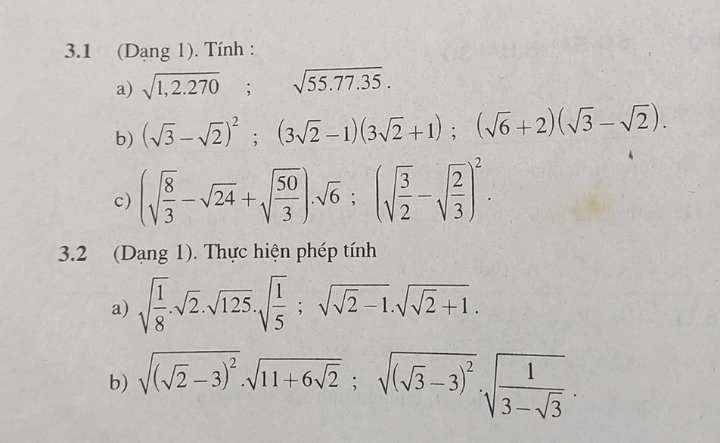
 giúp em giải chi tiết với ạ
giúp em giải chi tiết với ạ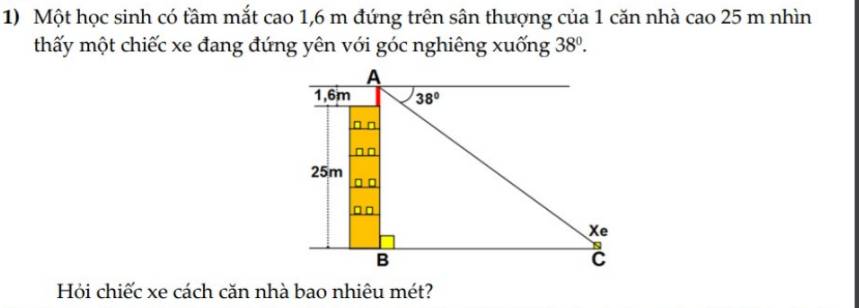



a, \(\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}-3}\)
\(=\dfrac{\sqrt{3}-3}{9-5\sqrt{3}}-\dfrac{\sqrt{3}-2}{9-5\sqrt{3}}\)
\(=\dfrac{-1}{9-5\sqrt{3}}\)
b, \(\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right)\cdot\left(\sqrt{x}-\dfrac{4}{\sqrt{x}}\right)\) (ĐK: x > 0; \(x\ne1\) )
\(=\left(\dfrac{x-3\sqrt{x}+2}{x-4}-\dfrac{x+4\sqrt{x}+4}{x-4}\right)\cdot\left(\dfrac{x}{\sqrt{x}}-\dfrac{4}{\sqrt{x}}\right)\)
\(=\left(\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-4}{x-4}\right)\cdot\left(\dfrac{x-4}{\sqrt{x}}\right)\)
\(=\dfrac{-7\sqrt{x}-2}{x-4}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{-7\sqrt{x}-2}{\sqrt{x}}\)
c, \(\dfrac{1}{\sqrt{x}-1}-\dfrac{3}{x\sqrt{x}-1}+\dfrac{1}{x+\sqrt{x}+1}\) (ĐK: \(x\ge0;x\ne1\) )
\(=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}\right)^3-1^3}-\dfrac{3}{\left(\sqrt{x}\right)^3-1^3}+\dfrac{\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{x+\sqrt{x}+1-3+\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{2\sqrt{x}+x-3}{\left(\sqrt{x}\right)^3-1^3}\)
P/s: vì chữ bạn hơi xấu, mình dịch chưa chắc đúng nên có gì sai bạn thông cảm nhé. ^^