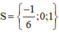K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
18 tháng 7 2019
a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
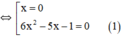
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm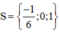 
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
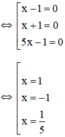
Vậy phương trình có tập nghiệm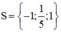 
SG
3
HY
7 tháng 4 2017
a, \(1,2x^3-x^2-0,2x=0\)
\(\Leftrightarrow12x^3-10x^2-2x=0\)
\(\Leftrightarrow6x^3-5x^2-x=0\)
\(\Leftrightarrow x\left(6x^2-5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\6x^2-5x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-\dfrac{1}{6}\end{matrix}\right.\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{-\dfrac{1}{6};0;1\right\}\)
b, \(5x^3-x^2-5x+1=0\)
\(\Leftrightarrow x^2\left(5x-1\right)-\left(5x-1\right)=0\)
\(\Leftrightarrow\left(5x-1\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=0\\5x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm1\\x=\dfrac{1}{5}\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-1;\dfrac{1}{5};1\right\}\)
10 tháng 4 2017
\(a,1,2x^3-x^2-0,2x=0\Leftrightarrow x\left(1,2x^2-x-0,2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\1,2x^2-x-0,2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{-1}{6}\end{matrix}\right.\)
\(b,5x^3-x^2-5x+1=0\Leftrightarrow x^2\left(5x-1\right)-\left(5x-1\right)=0\Leftrightarrow\left(5x-1\right)\left(x-1\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=1\\x=-1\end{matrix}\right.\)
CM
4 tháng 11 2019
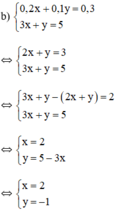
Vậy hệ phương trình có nghiệm duy nhất (2; -1).
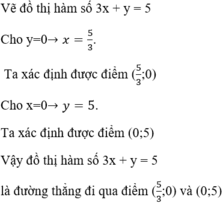
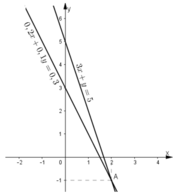
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
PT
1
CM
15 tháng 11 2018
a ) x 2 – 5 = 0 ⇔ x 2 = 5 ⇔ x 1 = √ 5 ; x 2 = - √ 5
Vậy phương trình có hai nghiệm x 1 = √ 5 ; x 2 = - √ 5
Cách khác:
x 2 – 5 = 0 ⇔ x 2 – ( √ 5 ) 2 = 0
⇔ (x - √5)(x + √5) = 0
hoặc x - √5 = 0 ⇔ x = √5
hoặc x + √5 = 0 ⇔ x = -√5
b)
x 2 – 2 √ 11 x + 11 = 0 ⇔ x 2 – 2 √ 11 x + ( √ 11 ) 2 = 0 ⇔ ( x - √ 11 ) 2 = 0
⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11
PT
1
CM
14 tháng 9 2019
4x4 + x2 – 5 = 0;
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
4t2 + t - 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t1 = 1; t2 =(-5)/4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x2 = 1 ⇔ x = ±1
Vậy phương trình có 2 nghiệm x1 = 1; x2 = -1
PT
1
CM
21 tháng 4 2017
a) 3 x 2 – 7x + 2 = 0
Δ= 7 2 -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5
Phương trình có 2 nghiệm phân biệt:
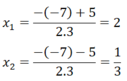
Vậy tập nghiệm của phương trình là S = {2; 1/3}
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
PT
1
CM
9 tháng 7 2017
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: x 4 -8 x 2 – 9 =0 ⇔ m 2 -8m -9 =0
Phương trình m 2 - 8m - 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0
suy ra: m 1 = -1 (loại) , m 2 = -(-9)/1 =9
Ta có: x 2 =9 ⇒ x= ± 3
Vậy phương trình đã cho có 2 nghiệm : x 1 =3 ; x 2 =-3
PT
1
CM
17 tháng 5 2017
Đặt m = x 2 – 2x
Ta có: x 2 - 2 x 2 – 2 x 2 + 4x – 3 = 0
⇔ x 2 - 2 x 2 – 2( x 2 – 2x) – 3 = 0
⇔ m 2 – 2m – 3 = 0
Phương trình m 2 – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: m 1 = -1, m 2 = 3
Với m = -1 ta có: x 2 – 2x = -1 ⇔ x 2 – 2x + 1 = 0
Phương trình x 2 – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0
Suy ra: x 1 = x 2 = 1
Với m = 3 ta có: x 2 – 2x = 3 ⇔ x 2 – 2x – 3 = 0
Phương trình x 2 – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: x 1 = -1, x 2 = 3
Vậy phương trình đã cho có 3 nghiệm: x 1 = 1, x 2 = -1, x 3 = 3
1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm