
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

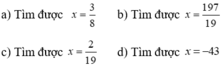

Câu 1 :
a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)
\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)
\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)
Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)
tương tự
\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)
\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)
\(< =>95-24x+40=6-4x-15x+5\)
\(< =>-24x+135=-19x+11\)
\(< =>5x=135-11=124\)
\(< =>x=\frac{124}{5}\)

a: =>3,6-1,7x=2,3-1,4-4=0,9-4=-3,1
=>1,7x=6,7
hay x=67/17
b: \(\Leftrightarrow30\left(5x+4\right)-15\left(3x+5\right)=24\left(4x+9\right)-40\left(x-9\right)\)
=>150x+120-45x-75=96x+216-40x+360
=>105x+45=56x+576
=>49x=531
hay x=531/49

a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27
a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27

Nhiều vậy ai làm hết được :P
1) \(\frac{3x-2}{3}-2=\frac{4x+1}{4}\)
\(\Leftrightarrow\frac{3x-8}{3}=\frac{4x-1}{4}\)
\(\Leftrightarrow4\left(3x-8\right)=3\left(4x-1\right)\)
\(\Leftrightarrow12x-32=12x-3\)(vô lí)
Vậy pt vô nghiệm
P/s: mấy câu sau tương tự thôi mà :)))
nhăm nhe 1 câu thôi
\(10,\frac{3+5x}{5}-3=\frac{9x-3}{4}\)
\(\Leftrightarrow\frac{3+5x-15}{5}=\frac{9x-3}{4}\)
\(\Leftrightarrow\frac{-12+5x}{5}=\frac{9x-3}{4}\)
\(\Leftrightarrow\left(-12+5x\right)5=\left(9x-3\right)4\)
\(\Leftrightarrow-60+25x=36x-12\)
\(\Leftrightarrow26x-36x=-12+60\)
\(\Leftrightarrow-10x=48\)
\(\Leftrightarrow x=-4,8\)

Bài 1:
a) (5x-4)(4x+6)=0
\(\Leftrightarrow\orbr{\begin{cases}5x-4=0\\4x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}5x=4\\4x=-6\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{4}{5}\\y=\frac{-3}{2}\end{cases}}}\)
b) (x-5)(3-2x)(3x+4)=0
<=> x-5=0 hoặc 3-2x=0 hoặc 3x+4=0
<=> x=5 hoặc x=\(\frac{3}{2}\)hoặc x=\(\frac{-4}{3}\)
c) (2x+1)(x2+2)=0
=> 2x+1=0 (vì x2+2>0)
=> x=\(\frac{-1}{2}\)
bài 1:
a) (5x - 4)(4x + 6) = 0
<=> 5x - 4 = 0 hoặc 4x + 6 = 0
<=> 5x = 0 + 4 hoặc 4x = 0 - 6
<=> 5x = 4 hoặc 4x = -6
<=> x = 4/5 hoặc x = -6/4 = -3/2
b) (x - 5)(3 - 2x)(3x + 4) = 0
<=> x - 5 = 0 hoặc 3 - 2x = 0 hoặc 3x + 4 = 0
<=> x = 0 + 5 hoặc -2x = 0 - 3 hoặc 3x = 0 - 4
<=> x = 5 hoặc -2x = -3 hoặc 3x = -4
<=> x = 5 hoặc x = 3/2 hoặc x = 4/3
c) (2x + 1)(x^2 + 2) = 0
vì x^2 + 2 > 0 nên:
<=> 2x + 1 = 0
<=> 2x = 0 - 1
<=> 2x = -1
<=> x = -1/2
bài 2:
a) (2x + 7)^2 = 9(x + 2)^2
<=> 4x^2 + 28x + 49 = 9x^2 + 36x + 36
<=> 4x^2 + 28x + 49 - 9x^2 - 36x - 36 = 0
<=> -5x^2 - 8x + 13 = 0
<=> (-5x - 13)(x - 1) = 0
<=> 5x + 13 = 0 hoặc x - 1 = 0
<=> 5x = 0 - 13 hoặc x = 0 + 1
<=> 5x = -13 hoặc x = 1
<=> x = -13/5 hoặc x = 1
b) (x^2 - 1)(x + 2)(x - 3) = (x - 1)(x^2 - 4)(x + 5)
<=> x^4 - x^3 - 7x^2 + x + 6 = x^4 + 4x^3 - 9x^2 - 16x + 20
<=> x^4 - x^3 - 7x^2 + x + 6 - x^4 - 4x^3 + 9x^2 + 16x - 20 = 0
<=> -5x^3 - 2x^2 + 17x - 14 = 0
<=> (-x + 1)(x + 2)(5x - 7) = 0
<=> x - 1 = 0 hoặc x + 2 = 0 hoặc 5x - 7 = 0
<=> x = 0 + 1 hoặc x = 0 - 2 hoặc 5x = 0 + 7
<=> x = 1 hoặc x = -2 hoặc 5x = 7
<=> x = 1 hoặc x = -2 hoặc x = 7/5

a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)

b)x+3=4:2
=> x=-1
d)5x-15=3x-5
<=> 5x-3x=15-5
<=> 2x=10
<=> x=5
f) 35-7x=11-5x
<=> 35-11=-5x+7x
<=> 24=2x
<=> x=12
h) 6x-2-3x=10
<=> 3x=10+2
<=> x=4
j)3-2x=3x+3-x-2
<=> 3-2x=2x+1
<=>-4x=-2
<=> x=1/2