Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)ĐK:\(\begin{cases}25x^2-9 \ge 0\\5x+3 \ge 0\\\end{cases}\)
`<=>` \(\begin{cases}(5x-3)(5x+3) \ge 0\\5x+3 \ge 0\\\end{cases}\)
`<=>` \(\begin{cases}\left[ \begin{array}{l}x\ge \dfrac35\\x \le -\dfrac35\end{array} \right.\\\end{cases}\)
`<=>` \(\left[ \begin{array}{l}x=-\dfrac35\\x \ge \dfrac35\end{array} \right.\)
`pt<=>\sqrt{5x+3}(\sqrt{5x-3}-2)=0`
`<=>` \(\left[ \begin{array}{l}5x+3=0\\\sqrt{5x-3}=2\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=-\dfrac35\\5x-3=4\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=-\dfrac35\\x=7/5\end{array} \right.\)
`b)sqrt{x-3}/sqrt{2x+1}=2`
ĐK:\(\begin{cases}x-3 \ge 0\\2x+1>0\\\end{cases}\)
`<=>x>=3`
`pt<=>sqrt{x-3}=2sqrt{2x+1}`
`<=>x-3=8x+4`
`<=>7x=7`
`<=>x=1(l)`
`c)sqrt{x^2-2x+1}+sqrt{x^2-4x+4}=3`
`<=>sqrt{(x-1)^2}+sqrt{(x-2)^2}=3`
`<=>|x-1|+|x-2|=3`
`**x>=2`
`pt<=>x-1+x-2=3`
`<=>2x=6`
`<=>x=3(tm)`
`**x<=1`
`pt<=>1-x+2-x=3`
`<=>3-x=3`
`<=>x=0(tm)`
`**1<=x<=2`
`pt<=>x-1+2-x=3`
`<=>=-1=3` vô lý
Vậy `S={0,3}`
\(a,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=-2\\ \Leftrightarrow-2\sqrt{x-1}=-2\Leftrightarrow\sqrt{x-1}=1\\ \Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\\ b,ĐK:x\ge0\\ PT\Leftrightarrow\dfrac{1}{3}\sqrt{2x}-2\sqrt{2x}+3\sqrt{2x}=12\\ \Leftrightarrow\dfrac{4}{3}\sqrt{2x}=12\Leftrightarrow\sqrt{2x}=9\\ \Leftrightarrow2x=81\Leftrightarrow x=\dfrac{81}{2}\left(tm\right)\)
c: Ta có: \(\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\)
\(\Leftrightarrow2\sqrt{x-1}=4\)
\(\Leftrightarrow x-1=4\)
hay x=5
e: Ta có: \(\sqrt{4x^2-28x+49}-5=0\)
\(\Leftrightarrow\left|2x-7\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=5\\2x-7=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)
a. ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{(x-2)^2}=2-x$
$\Leftrightarrow |x-2|=2-x$
$\Leftrightarrow 2-x\geq 0$
$\Leftrightarrow x\leq 2$
b. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{4}.\sqrt{x-2}-\frac{1}{5}\sqrt{25}.\sqrt{x-2}=3\sqrt{x-2}-1$
$\Leftrightarrow 2\sqrt{x-2}-\sqrt{x-2}=3\sqrt{x-2}-1$
$\Leftrightarrow 1=2\sqrt{x-2}$
$\Leftrightarrow \frac{1}{2}=\sqrt{x-2}$
$\Leftrightarrow \frac{1}{4}=x-2$
$\Leftrightarrow x=\frac{9}{4}$ (tm)
a) \(3x-2\sqrt{x-1}=4\) (ĐK: x ≥ 1)
\(\Rightarrow3x-2\sqrt{x-1}-4=0\)
\(\Rightarrow3x-6-2\sqrt{x-1}+2=0\)
\(\Rightarrow3\left(x-2\right)-2\left(\sqrt{x-1}-1\right)=0\)
\(\Rightarrow3\left(x-2\right)-2.\dfrac{x-2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow\left(x-2\right)\left[3-\dfrac{2}{\sqrt{x-1}+1}\right]=0\)
*TH1: x = 2 (t/m)
*TH2: \(3-\dfrac{2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow3=\dfrac{2}{\sqrt{x-1}+1}\)
\(\Rightarrow3\sqrt{x-1}+3=2\)
\(\Rightarrow3\sqrt{x-1}=-1\) (vô lí)
Vậy S = {2}
b) \(\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\) (ĐK: \(-\dfrac{1}{4}\le x\le3\) )
\(\Rightarrow\sqrt{4x+1}-3-\sqrt{x+2}+2-\sqrt{3-x}+1=0\)
\(\Rightarrow\dfrac{4x-8}{\sqrt{4x+1}+3}-\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{x-2}{\sqrt{3-x}+1}=0\)
\(\Rightarrow\left(x-2\right)\left(\dfrac{4}{\sqrt{4x+1}+3}-\dfrac{1}{\sqrt{x+2}+2}+\dfrac{1}{\sqrt{3-x}+1}\right)=0\)
=> x = 2
\(a,3x-2\sqrt{x-1}=4\left(x\ge1\right)\\ \Leftrightarrow-2\sqrt{x-1}=4-3x\\ \Leftrightarrow4\left(x-1\right)=16-24x+9x^2\\ \Leftrightarrow9x^2-28x+20=0\\ \Leftrightarrow\left(x-2\right)\left(9x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=\dfrac{10}{9}\left(tm\right)\end{matrix}\right.\)
\(b,\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\left(-\dfrac{1}{4}\le x\le3\right)\\ \Leftrightarrow4x+1+x+2-2\sqrt{\left(4x+1\right)\left(x+2\right)}=3-x\\ \Leftrightarrow-2\sqrt{\left(4x+1\right)\left(x+2\right)}=2-6x\\ \Leftrightarrow\sqrt{4x^2+9x+2}=3x-1\\ \Leftrightarrow4x^2+9x+2=9x^2-6x+1\\ \Leftrightarrow5x^2-15x-1=0\\ \Leftrightarrow\Delta=225+20=245\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15-\sqrt{245}}{10}=\dfrac{15-7\sqrt{5}}{10}\left(ktm\right)\\x=\dfrac{15+\sqrt{245}}{10}=\dfrac{15+7\sqrt{5}}{10}\left(tm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{15+7\sqrt{5}}{10}\)
a/ \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\) (ĐKXĐ : \(x\ge1\))
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow2\sqrt{x-1}=2\Leftrightarrow x-1=1\Leftrightarrow x=2\)
b/ \(\sqrt{9x^2+18}+2\sqrt{x^2+2}-\sqrt{25x^2+50}+3=0\)
\(\Leftrightarrow3\sqrt{x^2+2}+2\sqrt{x^2+2}-5\sqrt{x^2+2}+3=0\)
<=> 3 = 0 (vô lý)
=> pt vô nghiệm.
c/ \(\frac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\) (ĐKXĐ : x>-5/7)
\(\Leftrightarrow9x-7=7x+5\Leftrightarrow2x=12\Leftrightarrow x=6\)
d/ \(\frac{\sqrt{2x-3}}{\sqrt{x-1}}=2\) (ĐKXĐ : \(x\ge\frac{3}{2}\))
\(\Leftrightarrow2x-3=4\left(x-1\Leftrightarrow\right)2x=1\Leftrightarrow x=\frac{1}{2}\) (loại)
Vậy pt vô nghiệm.
a, \(\dfrac{1}{2}\sqrt{x-5}-\sqrt{4x-20+3}=0\left(dkxd:x\ge5\right)\)
\(< =>\dfrac{\sqrt{x-5}}{2}=\sqrt{4x-17}\)
\(< =>\dfrac{x-5}{4}=4x-17\)
\(< =>x-5=16x-68\)
\(< =>15x=68-5=63\)
\(< =>x=\dfrac{63}{15}=\dfrac{21}{5}\)(ktm)
b, \(\sqrt{2x+1}-2\sqrt{x}+1=0\left(dkxd:x\ge0\right)\)
\(< =>\sqrt{2x+1}+1=2\sqrt{x}\)
\(< =>2x+1+1+2\sqrt{2x+1}=4x\)
\(< =>2x-2\sqrt{2x+1}-2=0\)
\(< =>2x+1-2\sqrt{2x+1}+1-4=0\)
\(< =>\left(\sqrt{2x+1}-1\right)^2=4\)
\(< =>\left\{{}\begin{matrix}\sqrt{2x+1}-1=2\\\sqrt{2x+1}-1=-2\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}\sqrt{2x+1}=3\\\sqrt{2x+1}=-1\left(loai\right)\end{matrix}\right.\)
\(< =>2x+1=9< =>2x=8< =>x=4\)(tmdk)
a) 25x2 – 16 = 0 ⇔ 25x2 = 16 ⇔ x2 =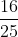
⇔ x = ±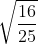
= ±
b) 2x2 + 3 = 0: Phương trình vô nghiệm vì vế trái là 2x2 + 3 ≥ 3 còn vế phải bằng 0.
c) 4,2x2 + 5,46x = 0 ⇔ 2x(2,1x + 2,73) = 0
=> x = 0
Hoặc 2,1x + 2,73 = 0 => x = -1,3
d) 4x2 - 2√3x = 1 - √3 ⇔ 4x2 - 2√3x – 1 + √3 = 0
Có a = 4, b = -2√3, b’ = -√3, c = -1 + √3
∆’ = (-√3)2 – 4 . (-1 + √3) = 3 + 4 - 4√3 = (2 - √3)2, √∆’ = 2 - √3
x1 =
= 
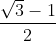, x2 = 
= 