Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
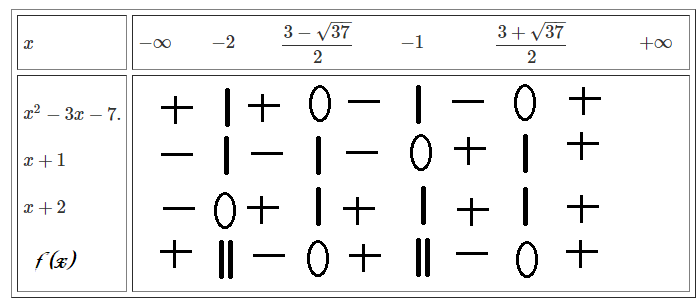
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

1: \(\Leftrightarrow\dfrac{3+2x-2}{x-1}>0\)
\(\Leftrightarrow\dfrac{2x+1}{x-1}>0\)
=>x>1 hoặc x<-1/2
2: \(\Leftrightarrow\dfrac{1-6x-2}{3x+1}< =0\)
\(\Leftrightarrow\dfrac{6x+1}{3x+1}>=0\)
=>x>1/3 hoặc x<=-1/6

1.
\(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-7\le x^2+1\\-4x^2-4\le x^2-2x-7\end{matrix}\right.\) (Do \(x^2+1>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{3}{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\-4\le x\le-\dfrac{3}{5}\end{matrix}\right.\)
2.
\(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+7\le13x^2-26x-26\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\) (Do \(x^2-5x+7>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\dfrac{11}{4}\\x\le-1\end{matrix}\right.\\x\le3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{11}{4}\le x\le3\\x\le-1\end{matrix}\right.\)
a: =>(x-1)(x-2)<=0
=>1<=x<=2
b: =>(x^2-1)(x^2-2)<=0
=>1<=x^2<=2
=>\(\left[{}\begin{matrix}1< =x< =\sqrt{2}\\-1>=x>=-\sqrt{2}\end{matrix}\right.\)