Question

[Lê Nam Khánh]

Giải bất phương trình sau: 

\(|\frac{x^2-3x-1}{x^2+x+1}|\)< 3 

Answer 1

[Quỳnh'ss Ok'ss]

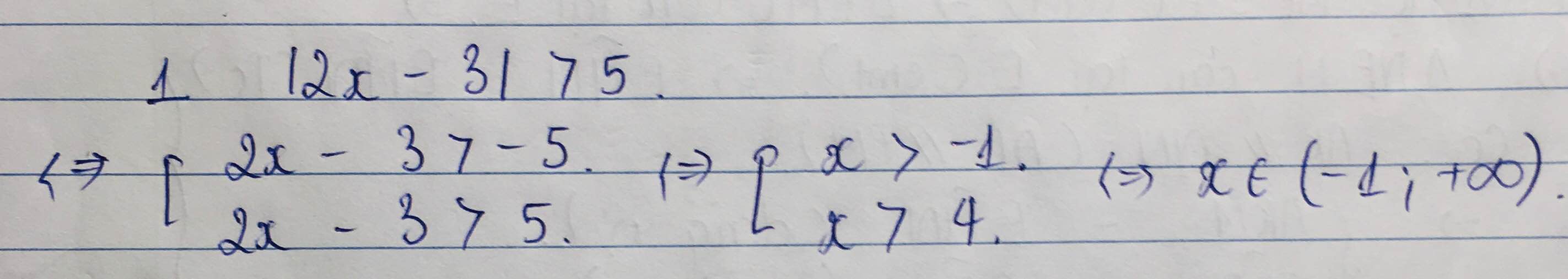
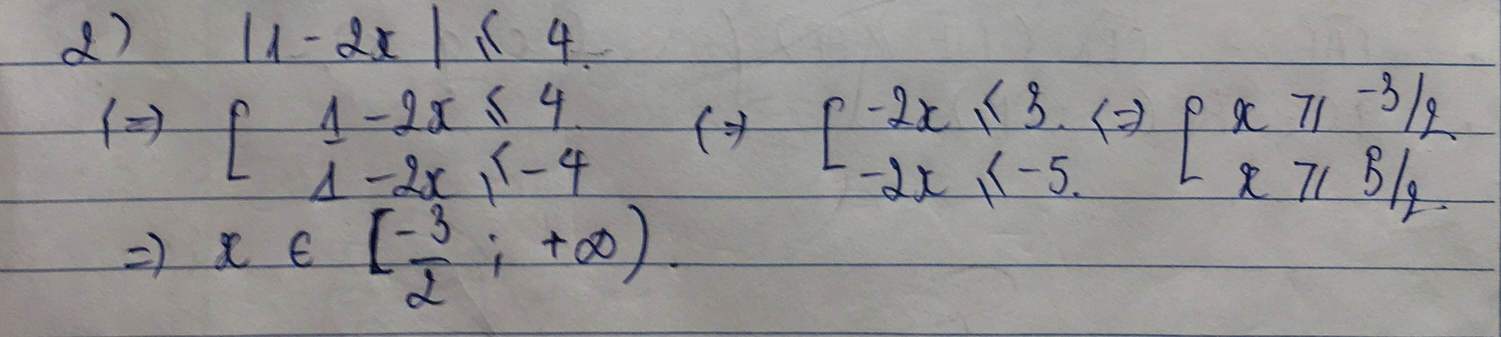
Bài làm

Ta có: \(\left|\frac{x^2-3x-1}{x^2+x+1}\right|< 3\)

\(\Leftrightarrow\hept{\begin{cases}\frac{x^2-3x-1}{x^2+x+1}< 3\\\frac{x^2-3x-1}{x^2+x+1}>-3\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\frac{x^2-3x-1}{x^2+x+1}-3< 0\\\frac{x^2-3x-1}{x^2+x+1}+3>0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\frac{x^2-3x-1}{x^2+x+1}-\frac{3x^2+3x+3}{x^2+x+1}< 0\\\frac{x^2-3x-1}{x^2+x+1}+\frac{3x^2+3x+3}{x^2+x+1}>0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\frac{-2x^2-6x-4}{x^2+x+1}< 0\\\frac{4x^2+2}{x^2+x+1}>0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\frac{-2\left(x+1\right)\left(x+2\right)}{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}< 0\\\frac{2\left(2x^2+1\right)}{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}>0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x\in\left(-\infty;1\right)U\left(2;+\infty\right)\\x\in\left(-\infty;+\infty\right)\end{cases}}\)

\(\Leftrightarrow x\in\left(-\infty;1\right)U\left(2;+\infty\right)\)