Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
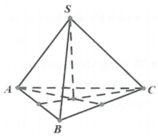
Áp dụng định lý Sin, ta có 2 R = A B sin A C B ^ ⇒ A B = 2 R . sin 60 ° = R 3 .
Và 2 R = B C sin B A C ^ ⇒ B C = 2 3 + 1 2 . Xét ∆ B H C vuông tại H, ta có
sin A C B ^ = B H B C ⇒ B H = sin 60 ° . B C = 6 + 3 2 4 R .
cos A C B ^ = C H B C ⇒ C H = cos 60 ° . B C = 6 + 2 4 R .
Khi quay ∆ B H C quanh trục AC ta được hình nón tròn xoay có bán kính đường tròn đáy r = BH và chiều cao h = C H = 6 + 2 4 R . Vậy S x q = πrl = 3 + 2 3 2 πR 2

Làm trên này là fai có cáh giải nuk cháu ak, ghi kq chỉ tổ tốn côg

BẠn chỉ mình vẽ bán kính trên hoc24.vn đi rồi mình giải cho

Đáp án B
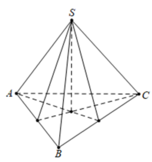
Áp dụng công thức tính diện tích tam giác S = p . r trong đó p là nửa chu vi và r là bán kính đường tròn nội tiếp tam giác

Đặt A B = A C = a , B C = b a , b > 0
Ta có: S A B C = p . r = p .1 = p = a + a + b 2 = a + b 2
Kẻ đường cao AH ta có: b 2 = a sin A 2 ⇒ S A B C = a + a sin A 2
Ta lại có S A B C = 1 2 a 2 sin A = a + a sin A 2 = a 1 + sin A 2
⇒ 1 2 a sin A = 1 + sin A 2 ⇔ a = 2 1 + sin A 2 sin A
⇒ S A B C = 2 1 + sin A 2 2 sin A 0 < A < π
Dùng M O D E 7 tìm GTNN của hàm số trên ta nhận được:
 Xấp xỉ
Xấp xỉ