
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Ta có: \(3\left(x-\dfrac{1}{2}\right)-3\left(x-\dfrac{1}{3}\right)=x\)
\(\Leftrightarrow x=3x-\dfrac{3}{2}-3x+1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
b: Ta có: \(-\dfrac{4}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{3}{2}\left(2x-1\right)\)
\(\Leftrightarrow x\cdot\dfrac{-4}{3}+\dfrac{1}{3}-3x+\dfrac{3}{2}=0\)
\(\Leftrightarrow x\cdot\dfrac{-13}{3}=-\dfrac{11}{6}\)
hay \(x=\dfrac{11}{26}\)

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O

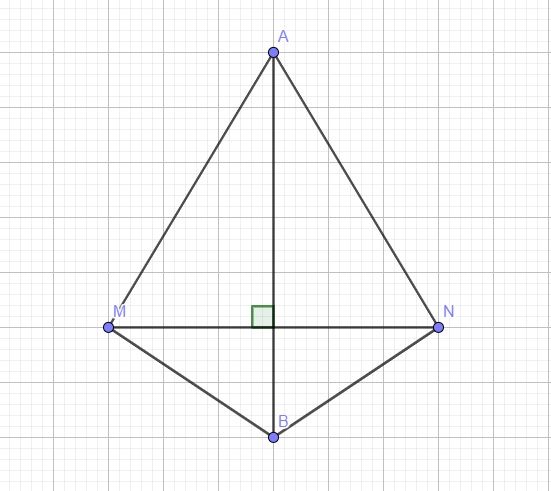
Do A thuộc trung trực đoạn MN nên \(AM=AN\)
Do B thuộc trung trực đoạn MN nên \(BM=BN\)
Xét 2 tam giác MAB và NAB có:
\(\left\{{}\begin{matrix}AM=AN\left(cmt\right)\\BM=BN\left(cmt\right)\\AB\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta MAB=\Delta NAB\left(c.c.c\right)\)

Bài 3:
a: Xét ΔCBA vuông tại B và ΔCHA vuông tại H có
CA chung
\(\widehat{BCA}=\widehat{HCA}\)
Do đó: ΔCBA=ΔCHA
Suy ra: CB=CH
hay ΔCBH cân tại C
b: Xét ΔBAF vuông tại B và ΔHAE vuông tại H có
AB=AH
\(\widehat{BAF}=\widehat{HAE}\)
Do đó: ΔBAF=ΔHAE
Suy ra: BF=HE
Xét ΔCFE có
CB/BF=CH/HE
nên BH//FE
c: Ta có: CF=CE
nên C nằm trên đường trung trực của EF(1)
Ta có: AF=AE
nên A nằm trên đường trung trực của FE(2)
Ta có: KF=KE
nên K nằm trên đường trung trực của FE(3)
Từ (1), (2) và (3) suy ra C,A,K thẳng hàng

\(a,-\left|2x-3\right|\le0,\forall x\Leftrightarrow-\left|2x-3\right|+3\le3\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(b,-\left|2-3x\right|\le0,\forall x\Leftrightarrow-\left|2-3x\right|-5\le-5\)
Dấu \("="\Leftrightarrow x=\dfrac{2}{3}\)
a: \(A=-\left|2x-3\right|+3\le3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
b: \(B=-\left|2-3x\right|-5\le-5\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)


a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
góc xOy là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB => góc AOD = góc BOC
=>góc BAI=gócDCI (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
góc DCI=góc ABI ( ∆AOD = ∆COB)
góc BAI=gócDCI (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> góc COI=gócAOI
=> OI là phân giác của góc xOy


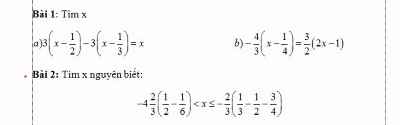 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ



:v chia ra đi bn
Câu 63:
a: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có
CA chung
AB=AE
=>ΔCAB=ΔCAE
b: Xét ΔCBE có
BH,CA là trung tuyến
BH cắt CA tại M
=>M là trọg tâm
c: Xét ΔCEB có
A là trung điểm của BE
AK//EC
=>K là trung điểm của BC
Xét ΔEBC có
M là trọng tâm
EK là trung tuyến
=>E,M,K thẳng hàng