Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 11:
=>4,6x=6,21
=>x=1,35
12: \(A=-\left(1.4-x\right)^2-1.4< =-1.4\)
=>x=-1,4
Câu 9:
\(\Leftrightarrow\dfrac{10a+b}{100c+90+d}=\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+...+\dfrac{1}{92}-\dfrac{1}{97}=\dfrac{1}{2}-\dfrac{1}{97}=\dfrac{95}{194}\)
=>a=9; b=5; c=1; d=4
=>a+b+c+d=9+5+1+4=19

`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`

Ta có: \(\left(x-\dfrac{1}{5}\right)^{2004}\ge0\forall x\)
\(\left(y+0.4\right)^{100}\ge0\forall y\)
\(\left(z-3\right)^{678}\ge0\forall z\)
Do đó: \(\left(x-\dfrac{1}{5}\right)^{2004}+\left(y+0.4\right)^{100}+\left(z-3\right)^{678}\ge0\forall x,y,z\)
Dấu '=' xảy ra khi
\(\left\{{}\begin{matrix}x-\dfrac{1}{5}=0\\y+0.4=0\\z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-\dfrac{2}{5}\\z=3\end{matrix}\right.\)
Vậy: (x,y,z)=\(\left(\dfrac{1}{5};-\dfrac{2}{5};3\right)\)

Ta có \(Q\left(1\right)=5-5+a^2-a=0\Leftrightarrow a\left(a-1\right)=0\Leftrightarrow\left[{}\begin{matrix}a=0\\a=1\end{matrix}\right.\)

Bài 1
1.\(x\left(x+3\right)\)
\(=x^2+3x\)
2.\(3x\left(x+2\right)\)
\(=3x^2+6x\)
3,\(x^2\left(3x-1\right)\)
\(=3x^3-x^2\)
4.\(-5x^3\left(3x^2-7\right)\)
\(=-15x^5+35x^3\)
5.\(3x\left(5x^2-2x-1\right)\)
\(=15x^3-6x^2-3x\)
6.\(-x^2\left(5x^3-x-\dfrac{1}{2}\right)\)
\(=-5x^5+x^3+\dfrac{x^2}{2}\)
7.\(\left(x^2+2x-3\right).\left(-x\right)\)
\(=-x^3-2x^2+3x\)
8.\(4x^3\left(-2x^2+4x^4-3\right)\)
\(=-8x^5+16x^7-12x^3\)
9.\(-5x^2\left(3x^2-2x+1\right)\)
\(=-15x^4+10x^3-5x^2\)
10.\(-4x^5\left(x^3-4x^2+7x-3\right)\)
\(=-4x^8+16x^7-28x^6+12x^5\)
11.\(\left(x+2\right)\left(x+3\right)\)
\(=x^2+3x+2x+6\)
12.\(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
13.\(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
14.\(\left(x-3\right)\left(x^2-2x-1\right)\)
\(x^3-2x^2-x-3x^2+6x+3\)
15.\(\left(2x-1\right)\left(x^2-5x+3\right)\)
\(=2x^3-10x^2+6x-x^2+5x-3\)
16.\(\left(x-5\right)\left(-x^2+x-1\right)\)
\(=-x^3+x^2-x+5x^2-5x+5\)
17,\(\left(\dfrac{1}{2}x+3\right)\left(2x^2-4x-6\right)\)
\(=x^3-2x^2-3x+6x^2-12x-18\)
P/s:mình làm hơi tắt tại bài dài quá:))

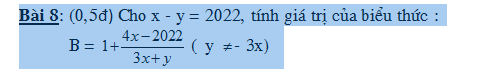 mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều
mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều 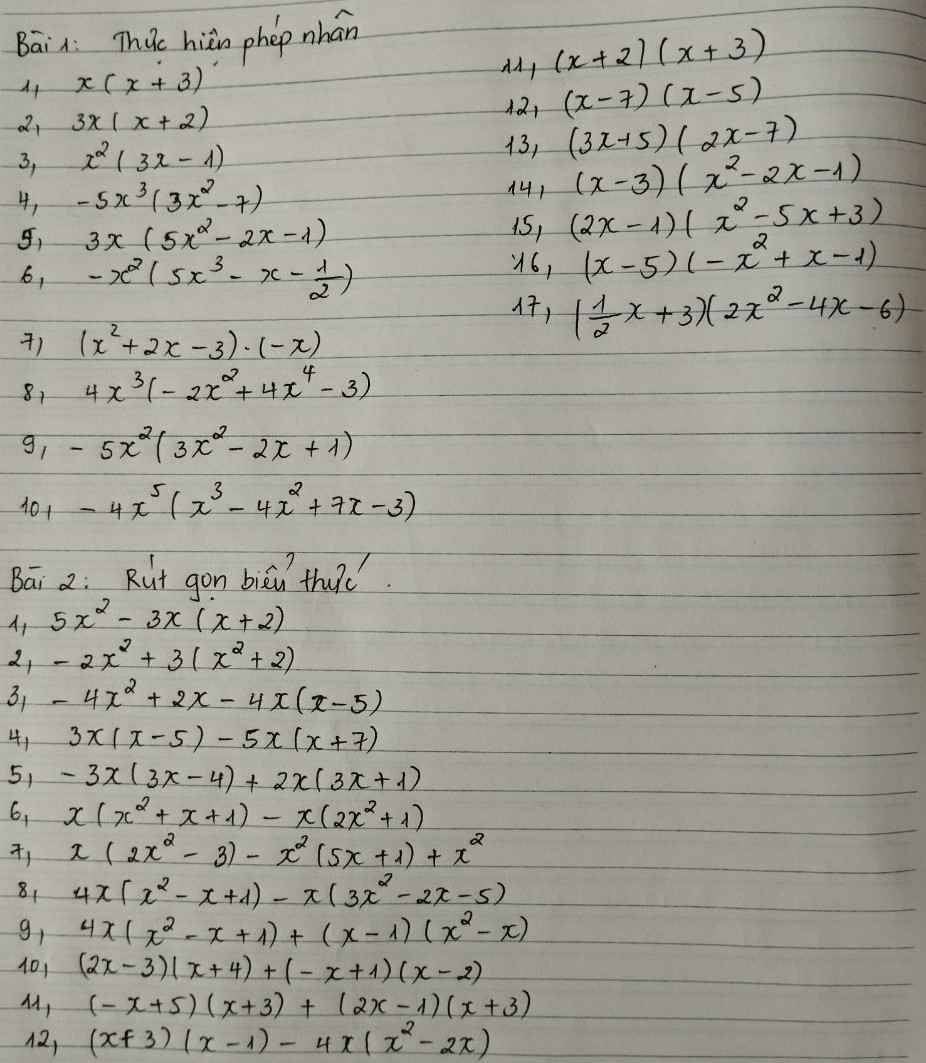
X = \(\frac{5.n+6.5+9.2+10.1}{n+5+2+1}=6,8\)
=> \(\frac{5n+30+18+10}{n+8}=6,8\)
=> \(\frac{5n+58}{n+8}=6,8\)
=> 5n + 58 = 6,8(n + 8)
=> 5n + 58 = 6,8n + 54,4
=> 5n - 6,8n = 54,4 - 58
=> -1,8n = -3,6
=> n = -3,6 : (-1,8)
=> m = 2