
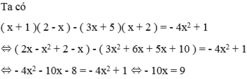

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

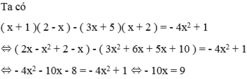


1 ) ( x^2 + 1 )( x^2 + 5 ) = 0
=> x^2 + 1 = 0 hoặc x^2 + 5 = 0
=> x^2 = -1 hoặc x^2 = -5 ( loại vì x^2 >= 0 )
2) =>20x^2 - 4x + 20x - 20x^2 = 16
=> 16x = 16
=> x = 1
3) ( 100 -a )( 100- b ) = 10000 - 100b - 100a - ab
= 100 ( 100 -a - b ) - ab
=> x = -1
sai
đọc kĩ đề bài 1 đi
số giá trị của x!
vậy9 kết quả phải là 0 vì x ko có kết quả nào thõa mản dk trên

1 ) \(\left(x^2+1\right)\left(x^2+5\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2+1=0\\x^2+5=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2=-1\\x^2=-5\end{array}\right.\) loại ( vì \(x^2\ge0\) )
Vậy không có giá trị nào thõa mãn .
2 ) \(4x\left(5x-1\right)+10x.\left(2-2x\right)=16\)
\(\Leftrightarrow20x^2-4x+20x-20x^2=16\)
\(\Leftrightarrow16x=16\)
\(\Leftrightarrow x=1\)
3 ) \(\left(100-a\right)\left(100-b\right)\)
\(=10000-100b-100a-ab\)
\(=100\left(100-a-b\right)-ab\)
\(\Rightarrow x=-1\)

vì x+y=4 nền (x+y)^2=4^2 =x^2+ 2xy+y^2=16 ma xy=5 nên 2xy=10 ta có x^2+y^2+10=16 ; x^2+y^2= 16-10 x^2+y^2=6 kết quả mik là z đó nhưng k biết có đúng k bn ak

Câu 6: Giá trị của biểu thức (x2 - 8) x (x + 3) - (x - 2) x (x + 5) tại x=-3là:
A.-4 B.16 C. -10 D. 10
Câu 7:Giá trị của biểu thức 6 + (x5 - 3) x (x3 + 2) - x8 - 2x5 tại x= -1/3 là:
A. -1/9 B. 1/9 C.9 D.-9

5.\(C\text{ó}x^2-12=0\Rightarrow x^2=12\Rightarrow x=\sqrt{12}ho\text{ặc}x=-\sqrt{12}\)
Mà x>0\(\Rightarrow x=\sqrt{12}\)
6.Vì x-y=4\(\Rightarrow\left(x-y\right)^2=x^2-2xy+y^2=x^2-10+y^2=4^2=16\Rightarrow x^2+y^2=26\)
Có \(\left(x+y\right)^2=x^2+2xy+y^2=26+10=36=6^2=\left(-6\right)^2\)
Vì xy>0 và x>0 =>y>0=>x+y>0=>x+y=6
7. \(3x^2+7=\left(x+2\right)\left(3x+1\right)\)
\(3x^2+7=3x^2+7x+2\)
\(3x^2+7-3x^2-7x-2=0\)
-7x+5=0
-7x=-5
\(x=\frac{5}{7}\)
8.\(\left(2x+1\right)^2-4\left(x+2\right)^2=9\)
\(\left(2x+1\right)^2-\left(2x+4\right)^2=9\)
(2x+1-2x-4)(2x+1+2x+4)=9
-3(4x+5)=9
4x+5=-3
4x=-8
x=-2
Còn câu 9 và 10 để mình nghiên cứu đã

Bài 1:
\(M=\left|x+13\right|+64\)
Vì \(\left|x+3\right|\ge0\)
=> \(\left|x+3\right|+64\ge64\)
Vậy GTNN của M là 64 khi x=-13
\(A=\left|x+3\right|+\left|x+5\right|=\left|-\left(x+3\right)\right|+\left|x+5\right|\)
Áp dụng bđt \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) ta có:
\(A\ge\left|-x-3+x+5\right|=2\)
Vaayj GTNN của A là 2 khi \(-3\le x\le5\)
Bài 2:
a) \(\left(x+10\right)^2=0\)
\(\Leftrightarrow x+10=0\Leftrightarrow x=-10\)
b) \(\left(x-\sqrt{121}\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x-\sqrt{121}=0\) (vì \(x^2+1>0\) )
\(\Leftrightarrow x=11\)
Bài 1:
a)Ta thấy: \(\left|x+13\right|\ge0\)
\(\Rightarrow\left|x+13\right|+64\ge64\)
\(\Rightarrow M\ge64\)
Dấu = khi x=-13
b)\(\left|x+3\right|+\left|x+5\right|=\left|x+3\right|+\left|-x-5\right|\)
Áp dụng Bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|x+3\right|+\left|-x-5\right|\ge\left|x+3+\left(-x\right)-5\right|=2\)
\(\Rightarrow A\ge2\)
Dấu = khi \(\left(x+3\right)\left(x+5\right)\ge0\)\(\Rightarrow3\le x\le5\)
\(\Rightarrow\begin{cases}\left(x+3\right)\left(x+5\right)=0\\3\le x\le5\end{cases}\)\(\Rightarrow\)\(\begin{cases}x=-3\\x=-5\end{cases}\)
Vậy MinA=2 khi \(\begin{cases}x=-3\\x=-5\end{cases}\)