Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x1,x2 là hai nghiệm \(\Rightarrow x_1+x_2=-a\) và \(x_1x_2=b+1\)
Ta có : \(a^2+b^2=\left[-\left(x_1+x_2\right)\right]^2+\left(x_1x_2-1\right)^2\)
\(\Rightarrow a^2+b^2=\left(x_1^2+x_2^2+2x_1x_2\right)+\left(x_1^2x_2^2-2x_1x_2+1\right)\)
\(\Rightarrow a^2+b^2=x_1^2+x_2^2+x_1^2x_2^2+1=\left(x_1^2+1\right)\left(x_2^2+1\right)\)là hợp số

Do pt có 1 nghiệm là \(2-\sqrt{3}\)
\(\Rightarrow\left(2-\sqrt{3}\right)^2+a\left(2-\sqrt{3}\right)+b=0\)
\(\Leftrightarrow7-4\sqrt{3}+2a-a\sqrt{3}+b=0\)
\(\Leftrightarrow2a+b+7=\left(a+4\right)\sqrt{3}\)
Vế trái là số hữu tỉ, vế phải vô tỉ nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}a+4=0\\2a+b+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-4\\b=1\end{matrix}\right.\)

đoạn sau là x2-ax-1/(2a2)=0 nha, viết thiếu.
@nguyenthanhtuan cái này là chứng minh mà bạn.

a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 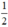
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 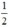
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 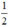
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 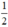 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 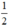 và vô nghiệm khi m >
và vô nghiệm khi m > 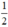

a: Δ=(2m+2)^2-4(m-2)
=4m^2+8m+4-4m+8
=4m^2+4m+12
=(2m+1)^2+11>=11>0
=>Phương trình luôn cóhai nghiệm phân biệt
b: x1^2+2(m+1)x2-5m+2
=x1^2+x2(x1+x2)-4m-m+2
=x1^2+x1x2+x2^2-5m+2
=(x1+x2)^2-2x1x2+x1x2-5m+2
=(2m+2)^2-(m-2)-5m+2
=4m^2+8m+4-m+2-5m+2
=4m^2+2m+8
=4(m^2+1/2m+2)
=4(m^2+2*m*1/4+1/16+31/16)
=4(m+1/4)^2+31/4>=31/4
Dấu = xảy ra khi m=-1/4

\(\Delta=a^2-4b=a^2-4\left(2008-a\right)=a^2+4a-8032\)
Để pt có nghiệm nguyên \(\Rightarrow\Delta\) là số chính phương
\(\Rightarrow a^2+4a-8032=k^2\)
\(\Leftrightarrow\left(a+2\right)^2-8036=k^2\)
\(\Leftrightarrow\left(a+2-k\right)\left(a+2+k\right)=8036\)
Mặt khác do \(\left(a+2-k\right)+\left(a+2+k\right)=2\left(a+2\right)\) chẵn nên ta chỉ cần xét các cặp ước cùng tính chẵn lẻ của 8036 là \(\left(4018;2\right);\left(2;4018\right);\left(-2;-4018\right);\left(-4018;-2\right)\)
\(\left\{{}\begin{matrix}a+2-k=4018\\a+2+k=2\end{matrix}\right.\) \(\Rightarrow a=2008\Rightarrow x^2+2008x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-2008\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a+2-k=2\\a+2+k=4018\end{matrix}\right.\) \(\Rightarrow a=2008\) giổng TH trên
\(\left\{{}\begin{matrix}a+2-k=-2\\a+2+k=-4018\end{matrix}\right.\) \(\Rightarrow a=-2012\Rightarrow x^2-2012x+4020=0\Rightarrow\left[{}\begin{matrix}x=2\\x=2010\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a+2-k=-4018\\a+2+k=-2\end{matrix}\right.\) \(\Rightarrow a=-2012\) giống TH trên
Vậy nghiệm nguyên của pt là \(x=\left\{0;2;2008;2010\right\}\)