
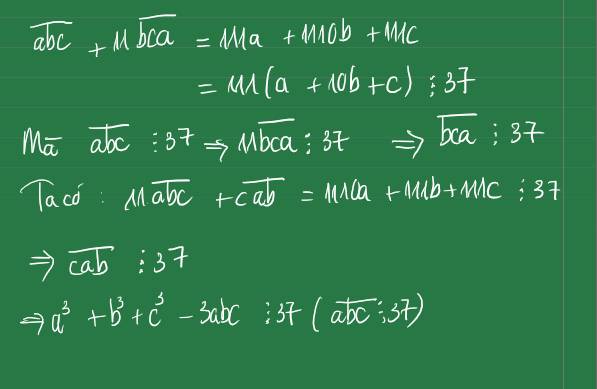
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

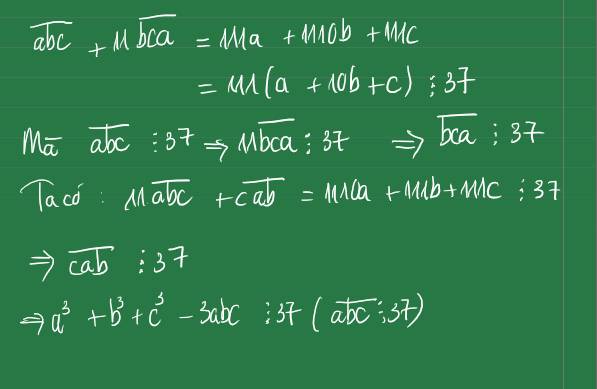

Ta có: \(\overline{abc}⋮37\Leftrightarrow100a+10b+c⋮37\)(1)
+) (1) => \(10\left(100a+10b+c\right)⋮37\)
<=> \(100b+10c+a+999a⋮37\) mà \(999a=37.27a⋮37\)
=> \(100b+10c+a⋮37\Leftrightarrow\overline{bca}⋮37\)
+) (1) => \(100\left(100a+10b+c\right)⋮37\)
<=> \(\left(100c+10a+b\right)+999\left(10a+b\right)⋮37\)mà \(999\left(10a+b\right)=37.27\left(10a+b\right)⋮37\)
=> \(\overline{cab}=100c+10a+b⋮37\)

Ta có \(\overline{abc}=100a+10b+c\)
\(\overline{bca}=100b+10c+a\)
\(\overline{cab}=100c+10a+b\)
Từ đó \(\Rightarrow\overline{abc}+\overline{bca}+\overline{cab}=100a+10b+c+100b+10c+a+100c+10a+b\)
\(=111a+111b+111c=111\left(a+b+c\right)\)
Mà 111 chia hết cho 37 nên \(\overline{abc}+\overline{bca}+\overline{cab}\)chia hết cho 37
ta thấy abc+bca+cab=111a+111b+111c
=111((a+b+c)=3x37x(a+b+c)chia hết cho 37

Theo đề, ta có: 100a+10b+c=11(a+b+c)
=>89a-b-10c=0
Do 10c+b<100 nên 89a<100
=>a<=1
=>a=1
=>89a=10z+y
=>z=8; y=9
=>198

Bài 2 :
a) \(10\le\overline{a_7a_8}\le31\) để \(100\le\left(\overline{a_7a_8}\right)^2\le999\) là số có ba chữ số.
Với mỗi số trong khoảng \(\left\{10;11;12;...;31\right\}\) ta lại có một số \(\overline{a_1a_2a_3}\) khác nhau; còn a4; a5; a6 tùy ý.
b) Trước hết : \(23\le\overline{a_7a_8}\le46\)
Trước hết để a7a8 khi lập phương lên sẽ vẫn có chữ số tận cùng ban đầu thì \(a_8\in\left\{0;1;4;5;6;9\right\}\)
Giả sử a8 = 0 thì số a4a5a6a7a8 chia hết cho 103 = 1000; hay a7 phải bằng 0; loại.
Nếu a8 = 1 thì xét \(23\le\overline{a_7a_8}\le46\) có số 31 không thỏa mãn.
Tương tự xét các trường hợp còn lại khi đã có giới hạn \(23\le\overline{a_7a_8}\le46\).
Bài 1 :
Không đủ dữ kiện.
Ngộ nhỡ m = n = 2 thì điều phải chứng minh là sai.

a = 1 => b = 10 => m = 60
a = 2 => b = 9 => m = 54
a = 3 => b = 8 => m = 48
a = 4 => b = 7 => m = 42
xyz = 60+54+48+42 = 204
Mật khẩu đầy đủ: math1204

Biến đổi đến 6c -5a = b tách b trừ c bằng 5 lần c trừ a suy ra b trừ c chia hết cho 5,
b >6,a <c lần lượt thay b bằng 7, 8, 9 tìm được c bằng 2, 3, 4 và a băng 1,2,3

Vì q=a2q=a2 nên ta có : q=1;4,9q=1;4,9
Với q=1q=1 ta có : abcd¯¯¯¯¯¯¯¯¯¯=dcba¯¯¯¯¯¯¯¯¯¯→a=b=c=dabcd¯=dcba¯→a=b=c=d
Mà abcd¯¯¯¯¯¯¯¯¯¯abcd¯ có dạng bình phương 1 số nguyên nên ta thử với các số có dạng xxxx¯¯¯¯¯¯¯¯¯¯¯=y2 (y∈Z)xxxx¯=y2 (y∈Z). Phương trình này vô nghiệm nên trường hợp này loại.
Với q=4q=4 ta có : abcd¯¯¯¯¯¯¯¯¯¯=4dcba¯¯¯¯¯¯¯¯¯¯abcd¯=4dcba¯
Có d chẵn, a≥9a≥9 nên d=2→a=8;9d=2→a=8;9
Tiếp tục thử với a=8; a=9a=8; a=9 bằng cách tách số hạng ta không tìm được số nào thỏa mãn.
Với q=9q=9 ta có a=9; d=1a=9; d=1 Tách tương tự không tìm được số nào thỏa mãn.
Nếu có chắc thử sai nhưng hướng làm là thế
