Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2.
Gọi x ( đồng ) là giá tiền của chiếc áo ban đầu
Giá tiền chiếc áo khi giảm 20% là:
x- ( x.20% ) = 0.8x (đồng)
Giá tiền của chiếc áo khi giảm thêm 5% nữa là:
0.8x- 0.8x.5% = 0.76x(đồng)
Giá tiền của chiếc áo ban đầu là:
0.76x = 266 000→ x=350 000 đồng
Vậy giá của chiếc áo ban đầu là 350k

Gọi độ dài chiều rộng của miếng đất hình chữ nhật là \(x\left(m\right),x>0\).
Vì chiều dài hơn chiều rộng là \(4\)mét nên độ dài chiều dài của miếng đất là: \(x+4\left(m\right)\).
Diện tích của miếng đất là \(x\left(x+4\right)\left(m^2\right)\)
Theo bài ra, ta có phương trình:
\(2x\left(x+4\right)=120\)
\(\Leftrightarrow x^2+4x-60=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=6\left(tm\right)\\x=-10\left(l\right)\end{cases}}\)
Vậy độ dài chiều rộng, chiều dài của miếng đất hình chữ nhật lần lượt là \(6\left(m\right),10\left(m\right)\).

Gọi x (m) là độ dài quãng đường tiếp theo Tuấn đi sau khi đi đc 600m đầu tiên (x>0)
Ta có pt:
12000 + 3000x = 87000
⇔3000x = 75000
⇔x = ?
Vậy quãng đường từ nhà → ngoại của Tuấn dài: 600 + x? = ?? (m)
Đổi ??m = ??? km.

gọi số tiền vật liệu , tiền công thợ mỗi m2 bác phải trả làx, y ( tr đ) ( 0<x,y<640/80=8)
số tiền công thợ bác phải trả theo dự tính là 80y (tr đ)
số tiền vât liệu bác phải trả theo dự tính là 80x (tr đ)
tổng số tiền phải trả theo dự tính là 80x + 80y = 640
x + y=8 (1)
thực tế diện tích ngôi nhà phải xây là 80 + 20 =100m2
thực tế số tiền phải trả là 100x + 8% . 100x + 100y + 15% . 100y = 868,2
108x + 115y = 868,2 (2)
từ 1 và 2 ta đc hpt \(\hept{\begin{cases}x+y=8\\108x+115y=868,2\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=7,4\\y=0,6\end{cases}}\)(tm)
vậy..................
ko bt có đúng ko nữa, cậu kiểm tra hộ tớ nha
#mã mã#

Đây là câu 21 của đề minh họa thị THPT QG 2017.
Lãi suất 12%/năm => lãi suất 1%/tháng.
Nếu còn nợ a đồng thì phải trả lãi 0,01 a cho 1 tháng.
Sau tháng đầu tiên, sau khi trả m đồng thì ông A còn nợ là:
(a + 0,01.a) - m = a. 1,01 - m
Sau tháng thứ hai, sau khi trả tiếp m đồng thì ông A còn nợ là:
(a . 1,01 - m) . 1,01 - m
Sau tháng thứ ba, sau khi trả tiếp m đồng thì ông A còn nợ là:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m
Con số nợ cuối cùng này phải bằng 0, suy ra:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m = 0
=> \(m=\frac{a.1,01^3}{1,01^2+1,01+1}=\frac{a.1,01^3\left(1,01-1\right)}{1,01^3-1}=\frac{a.1,01^3.0,01}{1,01^3-1}\)
Thay a = 100 vào ta có:
\(m=\frac{1,01^3}{1,01^3-1}\)

Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
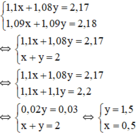
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.