
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(=\dfrac{3x-6+5x+10+3x-26}{\left(x-2\right)\left(x+2\right)}=\dfrac{11x-22}{\left(x-2\right)\left(x+2\right)}=\dfrac{11}{x+2}\)

Theo Wolfram ta có: (tự viết đề lại nhé)
\(3x^2+22x+40=0\)
\(\Leftrightarrow4x^2+24x+49=x^2+6x+9\)
\(\Rightarrow\orbr{\begin{cases}x=-4\\x=-\frac{10}{3}\end{cases}}\)
Ps: chả biết đúng hay sai!
\(\left(2x+7\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left(2x+7\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(2x+7-x-3\right)\left(2x+7+x+3\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x+10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\3x+10=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-4\\x=-\frac{10}{3}\end{cases}}\)
Vậy pt có 2 nghiệm x=-4,x=-10/3

Ta có : x + 2y + z + 2x + y + 2x = 5 + 9 + 10
<=> 3x + 3y + 3z = 24
<=> 3(x + y + z) = 24
=> x + y + z = 24 : 3 = 7

Nếu n lẻ thì n^3 và n là số lẻ
=> n^3 + n + 2 là số chẵn mà n lớn hơn hoặc bằng 1
=> n^3 + n + 2 là hợp số (1)
Nếu n chẵn thì n^3 và n là số chẵn
=> n^3 + n+2 là hợp số (2)
Từ (1) và (2) => n^3+n+2 là hợp số (đpcm!)

 giải hộ mik nha mik cần gấp ai nhanh mik tick
giải hộ mik nha mik cần gấp ai nhanh mik tick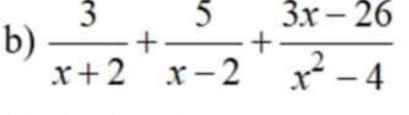 Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ
Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ