K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
HA
0
DT
5
2 tháng 11 2017
Có 2^285 = (2^3)^95 = 8^95
3^190 = (3^2)^95 = 9^95
Vì 8^95 < 9^95 nên 2^285 < 3^190
N
1
19 tháng 7 2018
8^12 =(2^3)^12 = 2^36
25^19 =(5^2)^19 = 5^38 = 5^36 .5^2 = 5^36 .25
Ta có: a.b = 2^36 .5^36 .25
= 10^36 .25
= 2500...000
36 c/s 0
Vậy a có 38 chữ số.
Chúc bạn học tốt.
TK
3
17 tháng 3 2018
Số đó là 266 ; 329 ; 392 ; 455 ; 518 ; 581 ; 644 ; 707 ; 770 ; 833 nha
18 tháng 11 2021
\(a,\Leftrightarrow2x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(b,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3+x>0\\2x-5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\2x-5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{5}{2}\\x< -3\end{matrix}\right.\)
\(c,\Leftrightarrow x\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-3< x< 0\)
\(d,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0\\x+5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\x+5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-3\\x< -5\end{matrix}\right.\)
\(e,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-2x\ge0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-2x\le0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x\le\dfrac{3}{2}\)
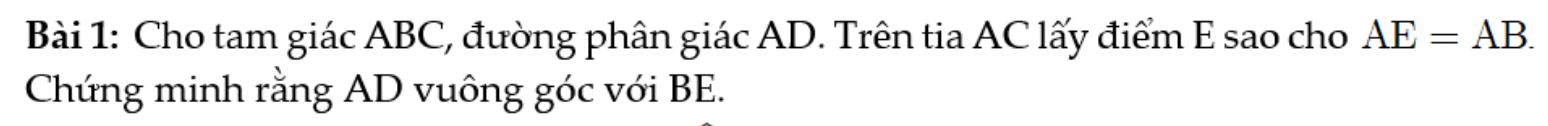
Xét tam giác ABE, có:
AB = AE ( gt )
=> Tam giác ABE cân tại A
Mà AD là tia phân giác
=> BE vuông góc với AD