Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
*Ta có:
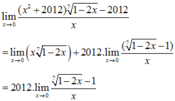
* Xét hàm số ![]() ta có
ta có ![]() .
.
Theo định nghĩa đạo hàm ta có:
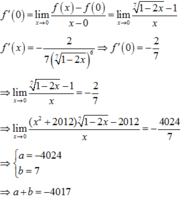

\(\lim\limits_{x\rightarrow1}\frac{\sqrt{5x-1}-2+2-\sqrt[3]{10x-2}}{\sqrt{2}\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{5\left(x-1\right)}{\sqrt{5x-1}+2}-\frac{10\left(x-1\right)}{4+2\sqrt[3]{10x-2}+\sqrt[3]{\left(10x-2\right)^2}}}{\sqrt{2}\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{1}{\sqrt{2}}\left(\frac{5}{\sqrt{5x-1}+2}-\frac{10}{4+2\sqrt[3]{10x-2}+\sqrt[3]{\left(10x-2\right)^2}}\right)=\frac{5}{12\sqrt{2}}=\frac{5}{3.2^2\sqrt{2}}\)
\(\Rightarrow\left\{{}\begin{matrix}a=5\\b=2\end{matrix}\right.\) \(\Rightarrow a+b=7\)

\(\lim\limits_{x\rightarrow1}\frac{x^{2016}+x-2}{\sqrt{2018x+1}-\sqrt{x+2018}}=\lim\limits_{x\rightarrow1}\frac{2016x^{2015}+1}{\frac{1009}{\sqrt{2018x+1}}-\frac{1}{2\sqrt{x+2018}}}=\frac{2017}{\frac{1009}{\sqrt{2019}}-\frac{1}{2\sqrt{2019}}}=2\sqrt{2019}\)
Để hàm liên tục tại \(x=1\)
\(\Rightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow k=2\sqrt{2019}\)
2.
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{x^2-1}=\frac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}a+b+1=0\\\lim\limits_{x\rightarrow1}\frac{2x+a}{2x}=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=-1\\\frac{a+2}{2}=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow S=1\)
3.
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{x^2+x+2}-2+2-\sqrt[3]{7x+1}}{\sqrt{2}\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{\left(x-1\right)\left(x+2\right)}{\sqrt{x^2+x+2}+2}-\frac{7\left(x-1\right)}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}}{\sqrt{2}\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{1}{\sqrt{2}}\left(\frac{x+2}{\sqrt{x^2+x+2}+2}-\frac{7}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\frac{3}{4}-\frac{7}{12}\right)=\frac{\sqrt{2}}{12}\)
\(\Rightarrow a+b+c=1+12+0=13\)

Bạn không nói rõ $n$ tiến tới đâu thì sẽ có nhiều kết quả. Căn cứ vào đáp án mình đoán $n\to +\infty$
Lời giải:
\(\lim\limits_{n\to +\infty}\frac{7\sqrt{3n^2+n}}{2(3n+2)}=\lim\limits_{n\to +\infty}\frac{\frac{7\sqrt{3n^2+n}}{n}}{\frac{2(3n+2)}{n}}=\lim\limits_{n\to +\infty}=\frac{7\sqrt{3+\frac{1}{n}}}{6+\frac{4}{n}}\)\(=\frac{7\sqrt{3}}{6}\)
$\frac{a}{b}$ tối giản $\Rightarrow a=7; b=6$
$\Rightarrow a+b=7+6=13$
Đáp án A.
Thiếu lim đúng không?