PT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 7 2021
`|x-2|=2x-3(x>=3/2)`
`<=>` \(\left[ \begin{array}{l}x-2=2x-3\\x-2=3-2x\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=1(l)\\3x=5\end{array} \right.\)
`<=>x=5/3(Tm(`
`2)A=-x^2+2x+9`
`=-(x^2-2x)+9`
`=-(x^2-2x+1)+1+9`
`=-(x-1)^2+10<=10`
Dấu "=" xảy ra khi `x=1.`
15 tháng 7 2021
1,
* \(|x-2|=x-2< =>x\ge2\)
\(=>x-2=2x-3< =>x=1\left(ktm\right)\)
*\(\left|x-2\right|=2-x< =>x< 2\)
\(=>2-x=2x-3< =>x=\dfrac{5}{3}\left(tm\right)\)
vậy x=5/3
2, \(A=-x^2+2x+9=-\left(x^2-2x-9\right)=-\left(x^2-2x+1-10\right)\)
\(=-\left[\left(x-1\right)^2-10\right]=-\left(x-1\right)^2+10\le10\)
dấu"=" xảy ra<=>x=1
17 tháng 8 2021
\(a)\)
\(\frac{1}{x+1}-\frac{x-1}{x}=\frac{3x+1}{x\left(x+1\right)}\)
\(\Leftrightarrow x-x^2+1=3x+1\)
\(\Leftrightarrow x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
\(b)\)
\(\frac{\left(x+2\right)^2}{2x-3}-\frac{1}{1}=\frac{x^2+10}{2x-3}\)
\(\Leftrightarrow x^2+4x+4-2x-3=x^2+10\)
\(\Leftrightarrow x^2+2x+1=x^2+10\)
\(\Leftrightarrow2x-9=0\)
\(\Leftrightarrow2x=9\)
\(\Leftrightarrow x=\frac{2}{9}\)
28 tháng 2 2022
a: \(A=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x+1}\right)\cdot\dfrac{\left(x+1\right)^2}{2x+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{2x+1}\)
\(=\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{2x+1}\)
\(=\dfrac{2x+1}{x-1}\cdot\dfrac{x+1}{2x+1}=\dfrac{x+1}{x-1}\)
b: Thay x=1/2 vào A, ta được:
\(A=\dfrac{\dfrac{1}{2}+1}{\dfrac{1}{2}-1}=\dfrac{3}{2}:\dfrac{-1}{2}=-3\)
c: Để A là số nguyên thì \(x-1+2⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow x\in\left\{2;0;3\right\}\)
DD
Đoàn Đức Hà
Giáo viên
15 tháng 5 2021
1) \(2x-\left|6x-7\right|=-x+8\)
\(\Rightarrow\orbr{\begin{cases}2x-\left(6x-7\right)=-x+8\\2x-\left(-6x+7\right)=-x+8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-3x=1\\9x=15\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{5}{3}\end{cases}}\)
Thử lại đều không thỏa mãn.
Vậy phương trình vô nghiệm.
2) \(\frac{\left|x+2\right|}{2}-\frac{\left|x-1\right|}{3}=\frac{1}{4}+\frac{x+3}{6}\)(2)
Với \(x\ge1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{x-1}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow0x=-\frac{7}{12}\)(phương trình vô nghiệm)
Với \(-2\le x< 1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{2}{3}x=\frac{1}{12}\Leftrightarrow x=\frac{1}{8}\)(thỏa mãn)
Với \(x< -2\): (2) tương đương với:
\(\frac{-x-2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{-1}{3}x=\frac{25}{12}\Leftrightarrow x=-\frac{25}{4}\)(thỏa mãn)
DD
Đoàn Đức Hà
Giáo viên
15 tháng 5 2021
3) \(\left|x^2-2x\right|=x\)
\(\Rightarrow\orbr{\begin{cases}x^2-2x=x\\x^2-2x=-x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-3x=0\\x^2-x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0,x=3\\x=0,x=1\end{cases}}\)
Thử lại đều thỏa mãn.
4) \(\left|x^2-4x+5\right|=x^2-1\)
\(\Leftrightarrow x^2-4x+5=x^2-1\)(vì \(x^2-4x+5=\left(x-2\right)^2+1>0\))
\(\Leftrightarrow-4x=-6\)
\(\Leftrightarrow x=\frac{3}{2}\)
LP
2
5 tháng 8 2021
Bài 1:
b) \(\left(2x^2-3y\right)^3\)
\(=8x^6-3\cdot4x^4\cdot3y+3\cdot2x^2\cdot9y^2-27y^3\)
\(=8x^6-36x^4y+54x^2y^2-27y^3\)
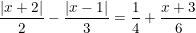
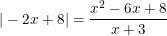
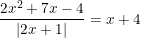
ĐK: x khác -1
\(\frac{2x-1}{x+1}=\frac{5\left(x+1\right)}{x+1}+\frac{3}{x+1}\)
\(\Leftrightarrow\frac{2x-1}{x+1}-\frac{5\left(x+1\right)}{x+1}-\frac{3}{x+1}=0\Leftrightarrow\frac{2x-1-5x-5-3}{x+1}=0=>\frac{-3x-9}{x+1}=-\frac{12}{x+1}=0\)
\(=>-3x-9=0=>x=-3\)
Có (2x-1)/(x+1)=5+3/(x+1) (2x-1)/(x+1)=5(x+1)/(x+1)+3/(x+1) Suy ra:2x-1=5(x+1)+3 2x-1=5x+5+3 2x-1=5x+8 2x-5x=8+1 -3x=9 x=-3