Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=\dfrac{1}{2^2}+\dfrac{1}{\left(2.2\right)^2}+\dfrac{1}{\left(2.3\right)^2}+...+\dfrac{1}{\left(2.10\right)^2}\)
\(=\dfrac{1}{2^2}+\dfrac{1}{2^2.2^2}+\dfrac{1}{2^2.3^2}+...+\dfrac{1}{2^2.10^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\right)\)
\(< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\right)\)
\(=\dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{4}\left(2-\dfrac{1}{10}\right)< \dfrac{1}{4}.2=\dfrac{1}{2}\) (đpcm)

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm

\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)


\(\dfrac{2x-3}{4}.\dfrac{6}{5}=\dfrac{21}{10}\\ \Leftrightarrow\dfrac{2x-3}{4}=\dfrac{7}{4}\\ \Leftrightarrow2x-3=7\\ \Leftrightarrow2x=10\\ \Leftrightarrow x=5\)

Mình làm vầy không biết đúng không nha
1-1/2+1/2-1/3+1/3-1/4+...+1/x-1/x+1=2020/2021
1-1/x+1=2020/2021
1/x+1=1-2020/2021
1/x+1=1/2021
x+1=2021
x=2020 Vậy x = 2020
Mình làm vắn tắt nha nếu chưa hiểu hỏi tớ tớ chỉ các làm cho
nhớ like cho me nhé . chúc bn học tốt
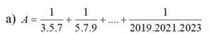
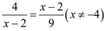
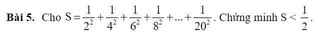
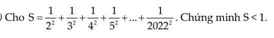
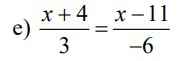

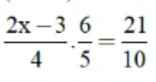

cái này thì triệt tiêu ra đó bn
là bằng 2020/6069