
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
a: \(BH=\sqrt{6^2-4.8^2}=3.6\left(cm\right)\)
\(CH=\dfrac{4.8^2}{3.6}=6.4\left(cm\right)\)
\(AC=\sqrt{6.4^2+4.8^2}=8\left(cm\right)\)
BC=10(cm)

Δ (delta) là viết tắt của "thay đổi". \(\Delta\) của phương trình hiểu đơn giản là sự thay đổi của phương trình.
delta là biệt thức của phương trình : \(\Delta=b^2-4ac\)
hay: \(\Delta'=b\) 2 - ac

3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8

Bạn chỉ cần vào cái ô đầu tiên trên thanh công cụ trên trang này là ghi được dấu căn rồi

Bài 2:
b. \(\sqrt{\left(3x+1\right)^2}=25\)
<=> \(|3x+1|=25\)
<=> \(\left[{}\begin{matrix}3x+1=-25\\3x+1=25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-26}{3}\\x=8\end{matrix}\right.\)
Bài 3:
Ta có: \(\dfrac{5}{\sqrt{7}+\sqrt{2}}+\dfrac{2}{3+\sqrt{7}}+\dfrac{2-\sqrt{2}}{\sqrt{2}-1}\)
\(=\sqrt{7}-\sqrt{2}+3-\sqrt{7}+\sqrt{2}\)
=3


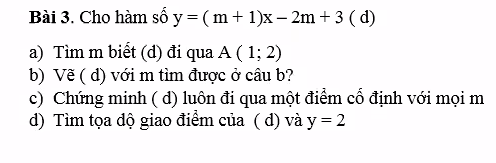 Ạ,GIÚP EM VỚI Ạ
Ạ,GIÚP EM VỚI Ạ








Bài 1:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
b.
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ (cm)
Áp dụng định lý Pitago:
$HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6$ (cm)
$HC=BC-HB=10-3,6=6,4$ (cm)
Hình bài 1:
