
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)

\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...

\(P=\dfrac{x^3+8y^3}{4^3+4^3}=\dfrac{\left(x+2y\right)^3-3\cdot x\cdot2y\cdot\left(x+2y\right)}{128}\)
\(=\dfrac{\left(-8\right)^3-6\cdot\left(-6\right)\cdot\left(-8\right)}{128}=\dfrac{128-6\cdot48}{128}=-\dfrac{5}{4}\)

xét :
|2x - 1| = 2x - 1 nếu 2x - 1 >0 hay x > \(\frac{1}{2}\)
=> 4(2x - 1) - x = 2 <=> 8x - 4 -x = 2 <=> 7x = 6 => x = \(\frac{6}{7}\)
( thỏa mãn ĐK )
|2x -1| = 1 - 2x nếu 2x - 1 < 0 hay x < \(\frac{1}{2}\)
=> 4.( 1 - 2x) - x = 2 <=> 4 - 8x -x = 2<=> 2 =9x => x = \(\frac{2}{9}\) (thỏa mãn ĐK)
vậy phương trình có nghiệm s = { \(\frac{1}{2},\frac{2}{9}\) }

a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC

Xét ΔDBM và ΔECM có
DB=EC
góc B=góc C
MB=MC
Do đó: ΔDBM=ΔECM
Suy ra: MD=ME(1)
Ta có: AD+DB=AB
AE+EC=AC
mà BD=CE và AB=AC
nên AD=AE(2)
Từ (1) và (2) suy ra AM là đường trung trực của DE
=>D đối xứng với E qua AM

1) \(x^3+y^3+z^3-3xyz=\left(x^3+3x^2y+3xy^2+y^3\right)+z^3-3xyz-3x^2y-3xy^2=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
2) Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
\(\Leftrightarrow ab+bc+ac=0\)
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^3b^3c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^2b^2c^2}=3\)
\(\Leftrightarrow a^3b^3+b^3c^3+a^3c^3=3a^2b^3c^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3ab^2c\left(ab+bc\right)+a^3b^3-3a^2b^2c^2=0\)
\(\Leftrightarrow\left(ab+bc+ac\right)\left[\left(ab+bc\right)^2-\left(ab+bc\right)ac+a^2c^2\right]-3ab^2c\left(ab+bc+ac\right)=0\)
\(\Leftrightarrow0+0=0\left(đúng\right)\)

\(1,7x-8=4x+7\)
\(\Leftrightarrow7x-8-4x=7\)
\(\Leftrightarrow7x-4x=7+8\)
\(\Leftrightarrow3x=15\)
\(\Rightarrow x=5\)
\(2,3-2x=3\left(x+1\right)-x-2\)
\(\Leftrightarrow3-2x=2x+1\)
\(\Leftrightarrow-2x+3=2x+1\)
\(\Leftrightarrow-2x-2x=1-3\)
\(\Leftrightarrow-4x=-2\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(3,5\left(3x+2\right)=4x+1\)
\(\Leftrightarrow5.3x+5.2=4x+1\)
\(\Leftrightarrow15x+10=4x+1\)
\(\Leftrightarrow15x-4x=1-10\)
\(\Leftrightarrow11x=-9\)
\(\Rightarrow x=\dfrac{-9}{11}\)



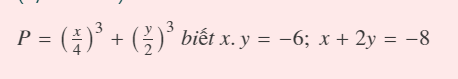

a: \(M=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
b: \(N=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
1. \(M=\dfrac{5}{x-1}-\dfrac{8}{x^2-1}-\dfrac{4}{x+1}\left(x\ne\pm1\right).\)
\(M=\dfrac{5\left(x+1\right)-8-4\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)\(M=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\)
\(M=\dfrac{1}{x-1}.\)
2. \(N=\dfrac{5}{x-1}+\dfrac{8}{1-x^2}-\dfrac{4}{x+1}\left(x\ne\pm1\right).\)
\(N=\dfrac{5\left(x+1\right)-8-4\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}\)
\(N=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}.\)
3. \(Q=\dfrac{1}{2x-1}-\dfrac{4}{4x^2-1}-\dfrac{2}{2x+1}\left(x\ne\pm\dfrac{1}{2}\right).\)
\(Q=\dfrac{2x+1-4-2\left(2x-1\right)}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x-3-4x+2}{\left(2x-1\right)\left(2x+1\right)}\)
\(Q=\dfrac{-2x-1}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{-1}{2x-1}.\)
4. \(F=\dfrac{x+3}{x-2}+\dfrac{x+2}{3-x}+\dfrac{x+2}{x^2-5x+6}\left(x\ne2,x\ne3\right).\)
\(F=\dfrac{x+3}{x-2}-\dfrac{x+2}{x-3}+\dfrac{x+2}{\left(x-3\right)\left(x-2\right)}\)
\(F=\dfrac{\left(x+3\right)\left(x-3\right)-\left(x+2\right)\left(x-2\right)+x+2}{\left(x-2\right)\left(x-3\right)}\)
\(F=\dfrac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}=\dfrac{x-3}{\left(x-2\right)\left(x-3\right)}\)
\(F=\dfrac{1}{x-2}.\)