Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có AM=MC=AC/2=10 cm ; IB=IC= BC/2 ; mà AC=BC (tam giáccân)
----> AM=MC=IB=IC=10 cm
Kéo dài CO cắt AB tại D
tam giác AOC có OA=OC (bán kính)
--> tam giác AOC cân tại O có OM là trung tuyến
---> OM vuông góc AC hay góc OMC=90 o
Tương tự với tam giác OCB được OI vuông góc BC hay góc OIC=90 o
Xét tam giác vuông OMC và tam giác vuông OIC:
MC=IC=10cm OC cạnh chung
--->tam giác OMC = tam giác OIC (ch.cgv)
--> góc MCO= góc ICO
---> CO hay CD là phân giác góc ACB của tam giác cân ABC
---> CD vuông góc AB hay góc ADC=90 o
AD=BD=AB/2 = 12 cm
Theo Pytago trong tam giác ACD:
CD^ 2= AC^ 2 -AD ^2 = 20 ^2 -12^ 2 =256
---> CD=16 cm
Đặt OC=OA=X
--> OD= CD-OC = 16 - X
Theo Pytago tam giác AOD:
AO2= OD^ 2+AD^ 2
<-->X^ 2= (16-X)^ 2 + 12 ^2
<--> 16^ 2 -32X + X^ 2 +12^ 2 - X ^2=0
<--> 400 - 32X=0
<--> X= -400/-32= 12,5 cm
Vậy bán kính đường tròn bằng 12,5 cm

a: Xét (O) có
OH là một phần đường kính
CD là dây
OH\(\perp\)CD tại H
Do đó: H là trung điểm của CD
Xét ΔACD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔACD cân tại A

Đáp án A
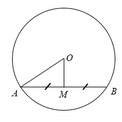
Vì M là trung điểm của AB nên ta có: 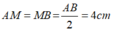
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
O M 2 = O A 2 - A M 2 = 52 - 42 = 9 ⇒ O M = 3 c m
giúp mình mỗi câu a thôi
giúp mình với