Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng d qua M có dạng: \(y=ax+b\)
Thế tọa độ M: \(1=a+b\Rightarrow b=1-a\Rightarrow y=ax+1-a\) với \(a\ne\left\{0;1\right\}\)
Tọa độ A: \(A\left(\dfrac{a-1}{a};0\right)\) ; tọa độ B: \(B\left(0;1-a\right)\) \(\Rightarrow a< 0\)
\(\Rightarrow OA=\dfrac{a-1}{a}\) ; \(OB=1-a\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=2\Leftrightarrow\left(\dfrac{a-1}{a}\right)\left(1-a\right)=4\)
\(\Leftrightarrow\left(a-1\right)^2+4a=0\Leftrightarrow a^2+2a+1=0\Rightarrow a=-1\)
\(\Rightarrow y=-x+2\)

Đáp án A
Gọi điểm A(a; 0) và B( 0; b)
+ Phương trình đoạn chắn (AB):
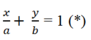
+Do tam giác OAB vuông cân tại O nên a = b do đó a= b hoặc a= -b.
+ TH1:b= a
Khi đó (*) trở thành: x a + y a = 1 hay x+ y= a
Mà M( 2; -3) thuộc AB nên 2-3= a hay a= -1; b= -1
Khi đó phương trình đường thẳng AB là: x+ y+ 1 = 0 .
+ TH2: b= -a
Khi đó (*) trở thành: x a - y a = 1 hay x- y= a
Mà M( 2; -3) thuộc AB nên 2+ 3= a hay a= 5; b= -5
Khi đó phương trình đường thẳng AB là: x- y- 5= 0

\(x=0\Rightarrow y=-2m+1\Rightarrow OA=\left|2m-1\right|\)
\(y=0\Rightarrow x=\dfrac{2m-1}{m-3}\Rightarrow OB=\left|\dfrac{2m-1}{m-3}\right|\)
\(\Delta OAB\) cân khi và chỉ khi \(\left|2m-1\right|=\left|\dfrac{2m-1}{m-3}\right|\)
\(\Leftrightarrow\left|2m-1\right|\left(\dfrac{1}{\left|m-3\right|}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=2\\m=\dfrac{1}{2}\end{matrix}\right.\)
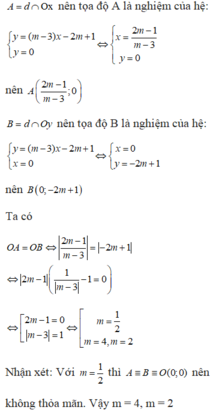
Ta có: \(\frac{1}{a}+\frac{1}{b}=1\Leftrightarrow ab=a+b\ge2\sqrt{ab}\)
\(\Rightarrow\sqrt{ab}\ge2\Rightarrow ab\ge4\)
Tọa độ \(A\left(0;b\right)\) ; \(B\left(a;0\right)\)
\(S=\frac{1}{2}ab\ge\frac{1}{2}.4=2\)
Dấu "=" xảy ra khi \(a=b=2\Rightarrow T=10\)