NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 7 2020
Số hữu tỉ là số viết được dưới dạng phân số a/b với a,b thuộc Z, b khác 0
VD: 0,6 ; -1,25 ; ...
Cách biểu diễn số hữu tỉ trên trục số là ( Mẹo )
- Nếu tử số < mẫu số thì ta biễu diễn số đó ở điểm 0 đến điểm 1
- Nếu tử số > mẫu số thì ta đưa về hỗn số , lấy phần nguyên làm điểm khoảng cách từ một số nào đó đến số nào đó
VD: Biểu diễn 5/4 trên trục số
- Chia đoạn thẳng đơn vị ( Chẳng hạn đoạn từ điểm 0 đến điểm 1 ) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng 1/4 đơn vị cũ...
So sánh số hữu tỉ .
VD; So sánh hỗn số \(-3\frac{1}{2}\) và 0
Ta có ; \(-3\frac{1}{2}\)= \(\frac{-7}{2}\) 0 = \(\frac{0}{2}\)
Vì -7 < 0 và 2 > 0 nên \(\frac{-7}{2}\)<\(\frac{0}{2}\). Vậy \(-3\frac{1}{2}\)< 0
hok tốt nhé...good luck
30 tháng 7 2020
UKkk... cảm ơn lời khuyên của bn ha...
Chúc...hok ... tốt nghen!
VD
8 tháng 4 2016
Trong toán học, căn bậc hai (√) của một số thực "a" là một số 'x' sao cho x2 = a, hoặc nói cách khác số x mà bình phương lên (kết quả của phép nhân với chính nó, hay x × x) là a.
ví dụ:
\(\sqrt{16}\)= 42 = 4*4
CM
2 tháng 4 2017
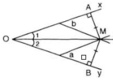
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
CM
4 tháng 1 2018
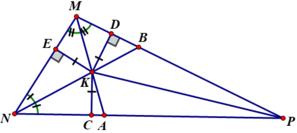
Điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau Theo định lí ⇒ K là giao điểm của các đường phân giác trong tam giác MNP.
Vì vậy ta chỉ cần vẽ phân giác của hai trong ba góc của ∆MNP.
Cách vẽ :
- Vẽ ΔMNP
- Vẽ đường phân giác của hai góc M và N : MA là phân giác góc M ; NB là phân giác góc B
Chúng cắt nhau tại K
- K là điểm cần vẽ
DN
0
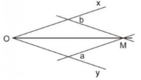
Đường phân giác trong là đường thẳng đi qua đỉnh của tam giác và chia góc đó thành hai góc bằng nhau.
Đường trung trực là đường thẳng xuất phát từ đỉnh đi qua trung điểm và vuông góc với cạnh đối diện của tam giác.