Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề: \(\dfrac{BC}{AB}=\dfrac{16}{9}\Rightarrow BC=\dfrac{16}{9}AB\)
Ta có: \(AC^2=AB^2+BC^2\Rightarrow AC=\sqrt{AB^2+BC^2}\)
\(=\sqrt{AB^2+\left(\dfrac{16}{9}AB\right)^2}=\sqrt{\dfrac{337}{81}AB^2}=\dfrac{\sqrt{337}}{9}AB\)
\(\Rightarrow50=\dfrac{\sqrt{337}}{9}AB\Rightarrow AB\approx24,5\) (inch) \(=62,23\left(cm\right)\)
\(\Rightarrow BC\approx110,6\left(cm\right)\)

3h41' = \(3\frac{41}{60}\)phút.
Gọi đoạn đường bằng là x.
tổng 2 đoạn đường lên dốc và xuống dốc là 9-x, người đó phải đi đoạn đường 9-x hai lần, một lần với vận tốc 4km/h, một lần vơí vận tốc 6km/h.
Ta có PT:
\(\frac{2x}{5}+\frac{9-x}{4}\frac{9-x}{6}=3\frac{41}{60}\)
Giải PT này ta được x=4.
Vậy đoạn đường bằng dài 4km.

Câu 3:
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
\(\widehat{BCE}\) chung
Do đó: ΔBEC\(\sim\)ΔADC
Suy ra: \(\dfrac{EC}{DC}=\dfrac{CB}{CA}\)
hay \(CE\cdot CA=CB\cdot CD\left(1\right)\)
Xét ΔBMC vuông tại M có MD là đường cao ứng với cạnh huyền BC
nên \(CD\cdot CB=CM^2\left(2\right)\)
Xét ΔANC vuông tại N có NE là đường cao ứng với cạnh huyền AC
nên \(CN^2=CE\cdot CA\left(3\right)\)
Từ (1), (2) và (3) suy ra CM=CN
hay ΔCMN cân tại C

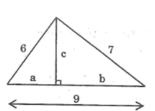
Gọi độ dài đường cao là c, hình chiếu của hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.
Ta có: a < b (vì 6 < 7)
Theo định lí Pi-ta-go, ta có:
c 2 = 6 2 - a 2 c 2 = 7 2 - b 2
Suy ra:
36 - a 2 = 49 - b 2 ⇔ b 2 - a 2 = 49 - 36
⇔ (b + a)(b – a) = 13 (*)
Mà x + y = 9 nên:
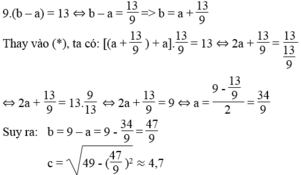

Gọi 2 đoạn dây có độ dài lần lượt là a ; b ( b < a < 0 )
Theo bài ra ta có \(\dfrac{a}{b}=\dfrac{5}{9}\Rightarrow\dfrac{a}{5}=\dfrac{b}{9};b-a=16\)
Theo tc dãy tỉ số bằng nhau \(\dfrac{a}{5}=\dfrac{b}{9}=\dfrac{b-a}{9-5}=\dfrac{16}{4}=4cm\Rightarrow a=20cm;b=36cm\)

a, A n B ⏜ - cung lớn; A m B ⏜ - cung nhỏ
Vì sđ A n B ⏜ + sđ A m B ⏜ = 360 0 ; mà sđ A n B ⏜ = 3sđ A m B ⏜
nên sđ A n B ⏜ = 270 0 và độ dài cung A n B ⏜ là l = 3 πR 2
b, Vì DOAB vuông cân => A O B ^ = 90 0 và O A B ^ = O B A ^ = 45 0
c, Vì AB = R 2 => OH = R 2 2 (OH ⊥ AB; H ∈ AB)

Gọi cạnh dài nhất là a ta có
Ta có √[p(p-a)(p-b)(p-c)]=(a*ha)/2 <=> ha=4*√110 /9 cái còn lại thì áp dụng định lý pytago là ra
bạn ơi,pải pik được mỗi bước bạn đi bao nhiêu cm và bàn chân bạn dài bao nhiêu thì mới pik dduocj độ dài chứ bạn
đề như vầy mk ko pik làm,mk xin lỗi