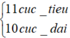Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là \(\frac{\lambda}{2} \Rightarrow \lambda = 2.2=4cm\)
Số gợn lồi (dao động cực đại) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< k \lambda < S_{1}S_{2}\Rightarrow -4.125 < k < 4.125\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4\)
=> có 9 gợn lồi.
Số gợn lõm (dao động cực tiểu) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< (k+0.5) \lambda < S_{1}S_{2}\Rightarrow -4.125 < k+0.5 < 4.125\\ \Rightarrow -4.625 < k < 3.625 \\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3.\)
=> có 8 gợn lõm.

Chọn đáp án B
Hai nguồn dao động cùng pha nên ta có điểm dao động với biên độ cực đại có:
d
1
-
d
2
=
k
λ
, vân trung trực ứng với vân cực đại bậc k=0.
Tại M có
d
1
=
30
c
m
,
d
2
=
25
,
5
c
m
, tại M là một vân cực đại, giữa M và trung trực của S1S2 có thêm một gợn lồi nữa như vậy ta có M ứng với vân cực đại bậc k=2
Từ đó ta có
λ
=
2
,
25
c
m
⇒
v
=
36
c
m

a)Trên \(O_1O_2\) dao động cùng pha có 14 dạng hyprbol mỗi bên
\(\Rightarrow2k+1=2\cdot14+1=29\) điểm cực đại.
Khoảng cách giữa chúng:
\(l=k\cdot\dfrac{\lambda}{2}=28\cdot\dfrac{\lambda}{2}=2,8\)
\(\Rightarrow\lambda=0,2cm\)
Vận tốc truyền sóng: \(v=\lambda\cdot f=0,2\cdot100=20\)cm/s

Chọn C
+ Khoảng cách giữa hai gợn lồi liên tiếp đúng bằng một bước sóng
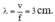

Bước sóng: \(\lambda=v/f=120/100=1,2(cm)\)
Số gợn sóng quan sát đc là: \(2.[\dfrac{S_1S_2}{\lambda}]+1=17\)
Tuy nhiện, vì 9,6 chia hết cho 1,2 nên ta trừ đi 2 điểm ở đầu mút, do vậy số gợn sóng quan sát đc là:
17-2=15 (gợn sóng)

Đáp án A
+ Các vị trí gợn lồi gặp gợn lồi → cực đại giao thoa, ngược lại các vị trí gợn lõm gặp gợn lõm là cực tiểu giao thoa
Đáp án: A
HD Giải:
Ta có: khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là 2cm → λ/2 = 2 → λ = 4cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số gợn lồi và lõm xuất hiện giữa hai điểm S1S2 là:
<=>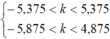
<=>