Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

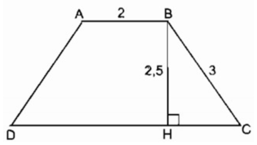
Cách dựng:
- Dựng ∆ BHC, BH = 2,5 cm
- ∠ (BHC) = 90 0
- Trên tia Hx lấy điểm C sao cho BC = 3cm
- Dựng tia đi qua B và song song CH nằm trên nửa mặt phẳng bờ BC chứa điểm H. Lấy điểm A sao cho BA = 2cm
- Dựng cung tròn tâm B bán kính bằng AC cắt tia CH tại D.
Nối AD ta có hình thang ABCD cần dựng.
Chứng minh: Thật vậy theo cách dựng AB // CD nên tứ giác ABCD là hình thang có AB = 2cm, BC = 3cm, BH = 2,5cm.
AC = BD
Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.



a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: ta có:ΔADB\(\sim\)ΔBCD
nên AD/BC=AB/BD
=>2,5/BC=1/2
hay BC=5(cm)

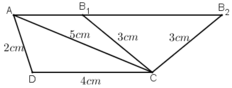
* Dựng hình:
- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.
- Dựng tia Ax song song với CD.
- Đường tròn (C; 3cm) cắt Ax tại B1 và B2.
Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.
* Chứng minh
+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.
+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.
+ B ∈ (C; 3cm) ⇒ BC = 3cm.

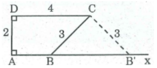
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn bài toán.
Ta thấy ∆ ADC xác định được vì biết AD = 2cm, ∠ D = 90 0 , DC = 4cm. Ta cần xác định đỉnh B. Đỉnh B thỏa mãn hai điều kiện:
- B nằm trên tia Ax//CD
- B cách C một khoảng bằng 3cm
Cách dựng:
- Dựng ΔADC biết:
AD = 2cm, ∠ D = 90 0 , DC = 4cm
- Dựng Ax ⊥ AD
- Dựng cung tròn tâm C bán kính bằng 3cm, cắt Ax tại B.
Nối BC ta có hình thang ABCD dựng được.
Chứng minh:
Thật vậy theo cách dựng, ta có: AB // CD , ∠ D = 90 0
Tứ giác ABCD là hình thang vuông
Lại có AD = 2cm, CD = 4cm, BC = 3cm
Hình thang dựng được thỏa mãn điều kiện bài toán.
Biện luận: ∆ ADC dựng được, hình thang ABCD luôn dựng được.
Bài toán có hai nghiệm hình.