Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(5\left(x^3-4x\right)=5x^3-20x\)
\(\left(10-5x\right)\left(-x^2-2x\right)=-10x^2-20x+5x^3+10x^2=5x^3-20x\)
\(\Leftrightarrow5\left(x^3-4x\right)=\left(10-5x\right)\left(-x^2-2x\right)\)
\(\Leftrightarrow\dfrac{x^3-4x}{10-5x}=\dfrac{-x^2-2x}{5}\)

a. \(x^2y^3.35xy=5.7x^3y^4\)
\(\Leftrightarrow35x^3y^4=35x^3y^4\Rightarrowđpcm\)
\(b.x^2\left(x+2\right).\left(x+2\right)=x\left(x+2\right)^2.x\)
\(\Leftrightarrow x^2\left(x+2\right)^2=x^2\left(x+2\right)^2\Rightarrowđpcm\)
\(c.\left(3-x\right)\left(9-x^2\right)=\left(3+x\right)\left(x^2-6x+9\right)\)
\(\Leftrightarrow\left(3-x\right)\left(3-x\right)\left(3+x\right)=\left(3+x\right)\left(3-x\right)^2\)
\(\Leftrightarrow\left(3-x\right)^2\left(3+x\right)=\left(3-x\right)^2\left(3+x\right)\)
\(\Rightarrowđpcm\)
\(d.5\left(x^3-4x\right)=\left(10-5x\right)\left(-x^2-2x\right)\)
\(\Leftrightarrow5x^3-20x=5x^3-20x\Rightarrowđpcm\)

\(\frac{x^2\left(x+2\right)}{x\left(x+2\right)^2}=\frac{x}{x+2}\Rightarrow\frac{x}{x+2}=\frac{x}{x+2}\)
\(\frac{3-x}{3+x}=\frac{x^2-6x+9}{9-x^2}\Rightarrow\frac{3-x}{3+x}=\frac{\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}\Rightarrow\frac{3-x}{3+x}=\frac{3-x}{3+x}\)
\(\frac{x^3-4x}{10-5x}=\frac{-x^2-2x}{5}\Rightarrow-\frac{x\left(x-2\right)\left(x+2\right)}{5\left(x-2\right)}=\frac{-x^2-2x}{5}\)
\(\Rightarrow\frac{-x\left(x+2\right)}{5}=\frac{-x^2-2x}{5}\Rightarrow\frac{-x^2-2x}{5}=\frac{-x^2-2x}{5}\)
k nha bạn
sai rồi cái này là dùng định nghĩa 2 phân thức bằng nhau để chứng minh chúng bằng nhau mà

pt <=> \(\left(x^2-x-2\right)\left(x-1\right)=\left(x+1\right)\left(x^2-3x+2\right)\)
\(\Leftrightarrow\left(x^2+x-2x-2\right)\left(x-1\right)=\left(x+1\right)\left(x^2-x-2x+2\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x-1\right)=\left(x+1\right)\left(x-2\right)\left(x-1\right)\)(Đúng \(\forall x\) )
Ta có:
\(\left(x^2-x-2\right)\left(x-1\right)\)
= \(\left(x^2-2x+x-2\right)\left(x-1\right)\)
= \([\left(x^2-2x)+(x-2\right)]\left(x-1\right)\)
= \([x\left(x-2)+(x-2\right)]\left(x-1\right)\)
= \(\left(x-2\right)\left(x+1\right)\left(x-1\right)\) (1)
Lại có:
\((x^2-3x+2)\left(x+1\right)\)
= \((x^2-2x-x+2)\left(x+1\right)\)
= \([(x^2-2x)-(x-2)]\left(x+1\right)\)
= \([x(x-2)-(x-2)]\left(x+1\right)\)
= \(\left(x-2\right)\left(x-1\right)\left(x+1\right)\) (2)
Từ (1), (2)
=> \(\left(x^2-x-2\right)\left(x-1\right)\) = \((x^2-3x+2)\left(x+1\right)\)
=> \(\dfrac{x^2-x-2}{x+1}=\dfrac{x^2-3x+2}{x-1}\)

Xin được mạn phép chữa đề.
\(\text{c) }\dfrac{x+2}{x+1}=\dfrac{\left(x+2\right)\left(x-1\right)}{x^2-1}\)
\(\text{Ta có : }\dfrac{\left(x+2\right)\left(x-1\right)}{x^2-1}=\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+2}{x+1}\left(đpcm\right)\)
Vậy.......................
c) x+2x+1=(x+2)(x−1)x2−1c) x+2x+1=(x+2)(x−1)x2−1
Ta có : (x+2)(x−1)x2−1=(x+2)(x−1)(x−1)(x+1)=x+2x+1(đpcm)
Vậy

a: \(\dfrac{7x^3y^4}{35xy}=\dfrac{7xy\cdot x^2y^3}{7xy\cdot5}=\dfrac{x^2y^3}{5}\)
b: \(\dfrac{x^3-4x}{10-5x}=\dfrac{-x\left(x-2\right)\left(x+2\right)}{5\left(x-2\right)}=\dfrac{-x\left(x+2\right)}{5}=\dfrac{-x^2-2x}{5}\)
c: \(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x+2}{x-1}\)
d: \(\left(x^2-x-2\right)\left(x-1\right)\)
\(=\left(x-2\right)\left(x+1\right)\left(x-1\right)\)
\(=\left(x^2-3x+2\right)\left(x+1\right)\)
=>\(\dfrac{x^2-x-2}{x+1}=\dfrac{x^2-3x+2}{x-1}\)
e: \(\dfrac{x^3+8}{x^2-2x+4}=\dfrac{\left(x+2\right)\left(x^2-2x+4\right)}{x^2-2x+4}=x+2\)

a) Ta có:
5y.28x = 140xy
7.20xy = 140xy
⇒ 5y.28x = 7.20xy
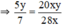
b) Ta có:
3x(x + 5).2 = 6x(x + 5)
2(x + 5). 3x = 6x(x + 5)
⇒ 3x(x + 5).2 = 2(x + 5).3x
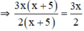
c) Ta có:
(x + 2).(x2 – 1) = (x + 2)(x – 1)(x + 1)
(x – 1).(x + 2)(x + 1) = (x + 2)(x – 1)(x + 1)
⇒ (x + 2).(x2 – 1) = (x – 1).(x + 2)(x + 1)
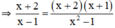
d) Ta có:
(x2 – x – 2)(x – 1)
= (x2 - 2x + x – 2).(x – 1)
= [x(x – 2) + (x – 2)].(x – 1)
= (x + 1)(x – 2)(x – 1)
(x + 1)(x2 – 3x + 2)
= (x + 1)(x2 – 2x – x + 2)
= (x + 1)[x.(x – 2) – (x – 2)]
= (x + 1)(x – 1)(x – 2)
= (x + 1)(x – 2)(x – 1)
⇒ (x2 – x – 2)(x – 1) = (x + 1)(x2 – 3x + 2)
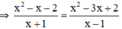
e) Ta có:
(x2 – 2x + 4).(x + 2) = (x + 2)(x2 – x.2 + 22) = x3 + 23 = x3 + 8
⇒ x3 + 8 = (x2 – 2x + 4)(x + 2)
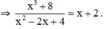
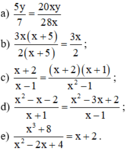
Ta có: \(\dfrac{x^3+8}{x^2-2x+4}=x+2\)
\(\Rightarrow\left(x^3+8\right)=\left(x^2-2.x+2^2\right)\left(x+2\right)\)
\(\Rightarrow x^3+8=x^3+8\)
\(\rightarrowđpcm.\)
Mình cảm ơn nha