Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét: Trong một tam giác, góc đối diện với cạnh lớn nhất là góc lớn nhất.
a) Cạnh c = 6cm lớn nhất nên góc lớn nhất là góc C:
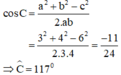
Vậy góc lớn nhất là 117º.
b) Cạnh a = 40cm lớn nhất suy ra góc lớn nhất là góc A:
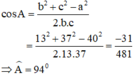
Vậy góc lớn nhất bằng 94º

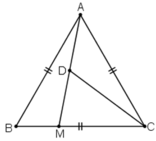
a) Do tam giác ABC là tam giác đều nên 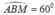 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
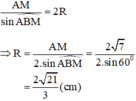
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
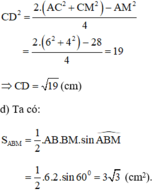

Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A
a) cos =
=
≈ -0,4583 =>
= 117016’
b)cos =
=
=>
= 93041’

a) tam giác cân nên dg cao cx là dg trung tuyến
=>BH=3
áp dụng pitago vs tam giác AHB tìm ra dc AH=4
b) vì AH cx là trung tuyến =>G thuộc AH =>A,G,H thẳng hàng
c) xét tam giác ABG và tam giác ACG có
BAH=HAC( dg cao cx là dg trung tuyến
AG chung
AB=AC
=>...

+)5cm;10cm;15cm: ko thể
+)4cm;12cm;13cm: có thể
+)8cm;8cm;8cm: có thể
+)10cm;13cm;13cm: có thể
tick nha!

Do a, b, c là độ dài ba cạnh của một tam giác nên theo bất đẳng thức tam giác ta có:
* a < b + c ⇔ a 2 < a b + c ⇔ a 2 < a b + a c
* a + c > b ⇔ b a + c > b 2 ⇔ a b + b c > b 2
* b - c < a ⇔ b - c 2 < a 2 ⇔ b 2 - 2 b c + c 2 < a 2 ⇔ b 2 + c 2 < a 2 + 2 b c
Do đó, mệnh đề D không đúng.
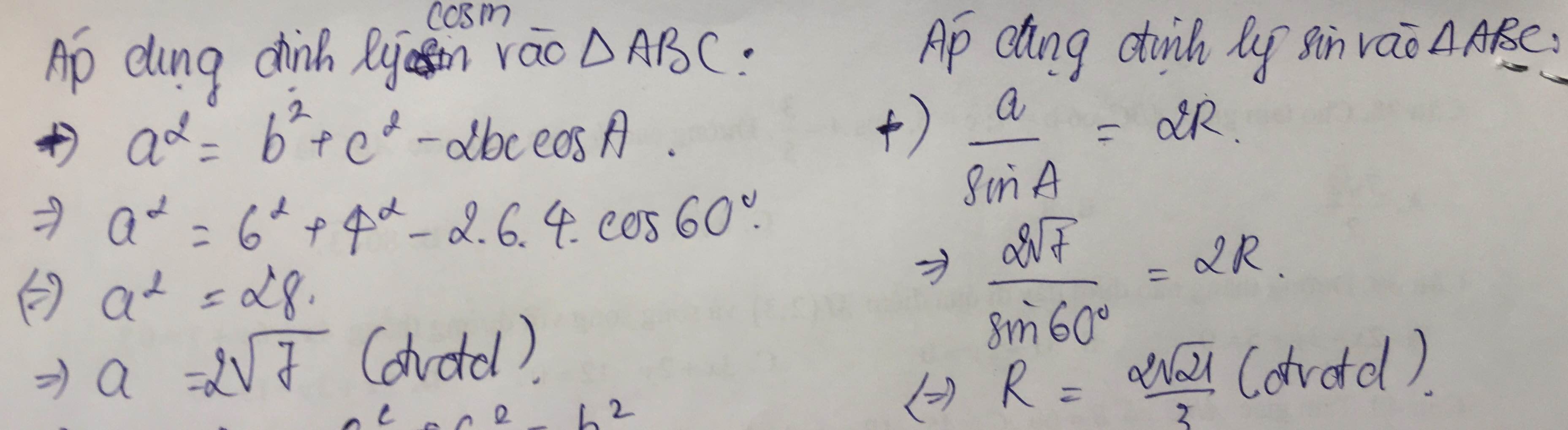
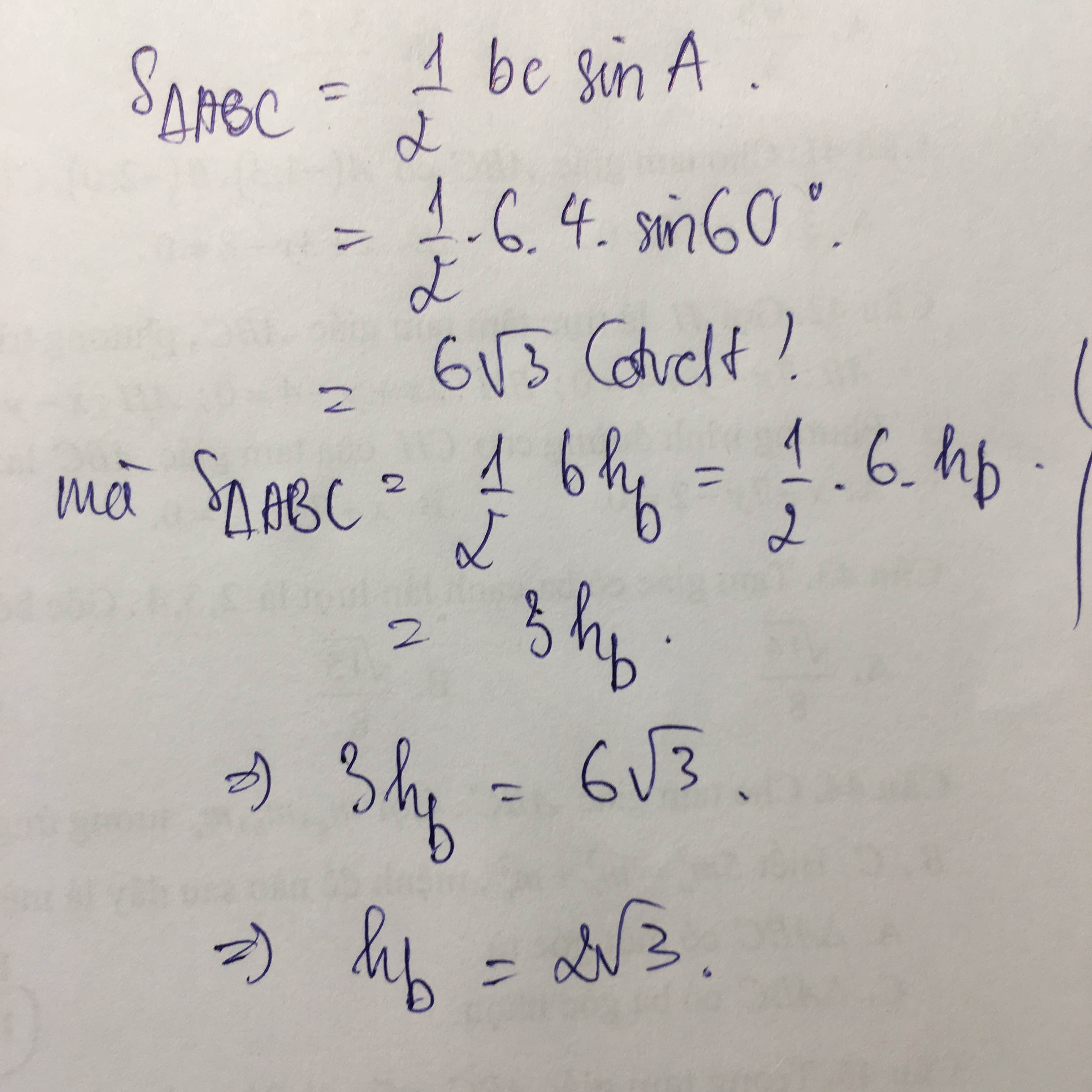
a;b
a) theo t/c của tg thì a+b>c mà 2+3=5 <6 nên 2;3;6 không thể là 3 cạnh của tg
b) tương tự