Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Số cách chọn 4 học sinh trong đội thanh niên xung kích là C 15 4 = 1365
Số cách chọn 4 học sinh sao cho mỗi khối có ít nhất một học sinh là
![]()
Vậy xác suất chọn được 4 học sinh sao cho mỗi khối có ít nhất một học sinh là
![]()

Đáp án A
Số cách chọn ngẫu nhiên 4 học sinh là: C 12 4 = 495
Gọi p là biến cố: 4 học sinh được chọn thuộc không quá 2 khối thì
p ¯ : 4 học sinh được chọn thuộc 3 khối
⇒ p ¯ = C 5 1 . C 4 1 . C 3 2 + C 5 1 . C 4 2 . C 3 1 + C 5 2 . C 4 1 . C 3 1 = 270
⇒ p = 1 − 270 495 = 5 11

Đáp án A
Số cách chọn ngẫu nhiên 4 học sinh là: C 12 4 = 495
Gọi p là biến cố: 4 học sinh được chọn thuộc không quá 2 khối thì
p ¯ : 4 học sinh được chọn thuộc 3 khối
⇒ p ¯ = C 5 1 . C 4 1 . C 3 2 + C 5 1 . C 4 2 . C 3 1 + C 5 2 . C 4 1 . C 3 1 = 270 ⇒ p ¯ = 1 - 270 495 = 5 11

Đáp án A
Chọn 4 học sinh có C 12 4 cách chọn.
Chọn 4 học sinh trong đó 4 học sinh được chọn có cả 3 khối có: C 5 2 C 4 1 C 3 1 + C 5 1 C 4 2 C 3 1 + C 5 1 C 4 1 C 3 2 = 270
Xác suất để 4 hoc sinh đươc chon có cả 3 khối là P = 270 C 12 4 = 6 11
Do đó xác suất sao cho 4 học sinh được chọn thuộc không quá 2 khối là 1 - 6 11 = 5 11 .

Chọn C.
Chọn ngẫu nhiên 6 học sinh trong 15 học sinh có C 15 6 cách ⇒ n Ω = C 16 5 .
Gọi X là biến cố “6 học sinh được chọn có đủ 3 khối” => biến cố đối X ¯ là “6 học sinh được chọn trong một khối hoặc hai khối”. Ta xét các trường hợp sau:
TH1. Chọn 6 học sinh từ một khối. Ta xét các trường hợp sau:
TH2. Chọn 6 học sinh từ hai khối, ta được
· 6 học sinh chọn từ khối 11 và 11 => có C 11 6 - C 6 6 cách
· 6 học sinh chọn từ khối 11 và 12 => có C 9 6 cách
· 6 học sinh chọn từ khối 12 và 10 => có C 10 6 - C 6 6 cách.
Vậy P = 1 - n X ¯ n Ω = 1 - 755 C 15 6 = 850 1001 .
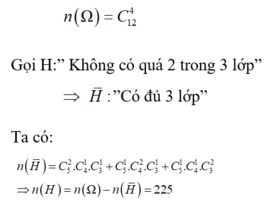

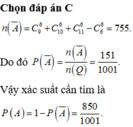
Đáp án C
TH1: 4 học sinh được chọn thuộc một lớp:
+ Lớp A có C 5 4 = 5 cách chọn.
+ Lớp B có C 4 4 = 1 cách chọn.
Trường hợp này có: 6 cách chọn.
TH2: 4 học sinh được chọn thuộc 2 lớp:
+ Lớp A và B: C 9 4 − C 5 4 + C 4 4 = 120 có .
+ Lớp B và C : C 7 4 − C 4 4 = 34 có
+ Lớp C và A: C 8 4 − C 5 4 = 65 có
Trường hợp này có 219 cách chọn.
Vậy có 225 cách chọn thỏa yêu cầu bài toán.