Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trên tia bd có
bc = 3cm < bd = 6 cm
=> c nằm giữa b và d (1)
=> bc + cd = bd
cd = bd -bc = 6 - 3=3 cm ( 2)
=> bc = cd
c) từ (1) và (2 ) => c là trung điểm của db
tick nha bạn

Tia đối của tia BA là tia BC
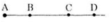
Trên tia BC có hai điểm C, D mà BC = 3cm < BD = 5cm nên C nằm giữa hai điểm B và D.
Do đó: BC + CD = BD suy ra CD = BD - BC = 5 - 3 = 2cm
Ta thấy: AB = 2cm = CD nên AB = CD.

Đáp án là C
![]()
Vì B nằm giữa A và C nên AB + BC = AC ⇒ AB = AC - BC = 5 - 3 = 2cm
Vì B nằm giữa A và C nên C thuộc tia đối của tia BA
Trên tia đối của tia BA có:
BC < BD, suy ra C nằm giữa B và D
⇒ BC + CD = BD ⇒ CD = BD - BC = 5 - 3 = 2cm
Vậy AB = CD

a) Vì B nằm giữa A và B nên ta có: AC - BC = AB
5 - 3=AB
2 =AB
Vậy AB = 2cm
b)Vì theo đề bài B nằm giữa A và C mà D năm trên tia đối của BD nên B nằm giữa C và D nên ta có:
BC + BD =CD
=> 3 + 6 =9 cm
Vì 9 > 6 nên CD > BD (đpcm)
c) vì B nằm giữa C và D nên C ko là trung điểm của BD (đpcm)
trên cùng một nửa mặt phẳng bờ chứa tia ox vẽ 3 điểm A B C SAO CHO OA =5cm
a. tính độ dài đoạn thẳng AB
b. so sánh AB và BC

a)Trên đoạn thẳng AC, có CB<CA(vì 3cm<5cm) nên B nằm giữa A và C
Ta có : AB+BC=AC
AB+ 3 =5
AB =5-3=2(cm)
b)Trên tia BD, có BC<BD(vì 3cm<6cm) nên C nằm giữa B và D
Ta có : BC+CD=BD
3 +CD=6
CD=6-3=3(cm)
\(\Rightarrow\)BC=CD=3cm
c) Vì C nằm giữa B và D và BC=CD nên C là trung điểm của đoạn DB
Tick cho mình nha bạn !