Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
x 4 − 3 x 2 + m = 0 ( 1 ) ⇔ x 4 − 3 x 2 − 3 = − 3 − m ( * )
Để phương trình (1) có 3 nghiệm phân biệt thì phương trình (*) có 3 nghiệm phân biệt
⇔ − 3 − m = − 3 ⇔ m = 0

Đáp án B
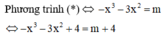
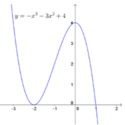
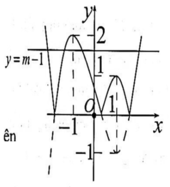
Số nghiệm của phương trình (*) chính là số giao điểm của đồ thị (C) với đường thẳng y = m + 4
Từ đồ thị hàm số y = - x 3 - 3 x 2 + 4 suy ra phương trình (*) có 2 nghiệm phân biệt
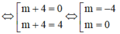

Đáp án D
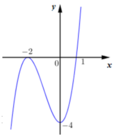
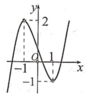
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

Chọn C.
Phương pháp: Số nghiệm của phương trình là số giao điểm của hai đường.

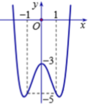
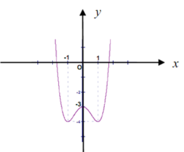


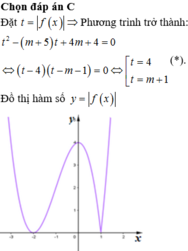






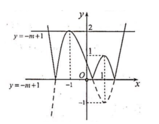
Chọn B.
Ta có:
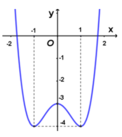
x 4 - 3 x 2 + m = 0 ⇔ x 4 - 3 x 2 = - m ⇔ x 4 - 3 x 2 - 3 = - m - 3 .
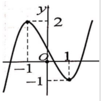
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi
- m - 3 = - 3 ⇔ m = 0 .