
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



PT : \(\sqrt{x^3-5}-\sqrt[3]{x^3+8}=1\) ( ĐKXĐ : \(x\ge\sqrt[3]{5}\))
\(\Leftrightarrow x^3+8=\left(\sqrt{x^3-5}-1\right)^3\)
\(\Leftrightarrow x^3+8=\left(\sqrt{x^3-5}\right)^3-3.\left(x^3-5\right)+3\sqrt{x^3-5}-1\)
\(\Leftrightarrow\left(\sqrt{x^3-5}\right)^3-4\left(x^3-5\right)+3\sqrt{x^3-5}-14=0\)
Đặt \(y=\sqrt{x^3-5},y\ge0\), pt trở thành \(y^3-4y^2+3y-14=0\)
Tới đây bạn tự giải !
\(a=\sqrt{x^3-5};\text{ }b=\sqrt[3]{x^3+8}\)
\(\Rightarrow\hept{\begin{cases}a-b=1\\b^3-a^2=x^3+8-\left(x^3-5\right)=13\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=b+1\\b^3-\left(b+1\right)^2=13\text{ (1)}\end{cases}}\)
\(\left(1\right)\Leftrightarrow b^3-b^2-2b-14=0\)
Nghiệm xấu rồi.

1
đặt biểu thức cần chứng minh là P
có \(\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{97}}.\sqrt{\left(a^2+\dfrac{1}{b^2}\right).\left(4^2+9^2\right)}\ge\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}\right)\)
là tương tự đối với \(\sqrt{b^2+\dfrac{1}{c^2}},\sqrt{c^2+\dfrac{1}{a^2}}\)
\(=>P\ge\)\(\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}+4b+\dfrac{9}{c}+4c+\dfrac{9}{a}\right)\)
(đến đây thấy đề sai sai vì ngược dấu )


rat de chay ra cho khac that nhanh va chui no di dung can than vao





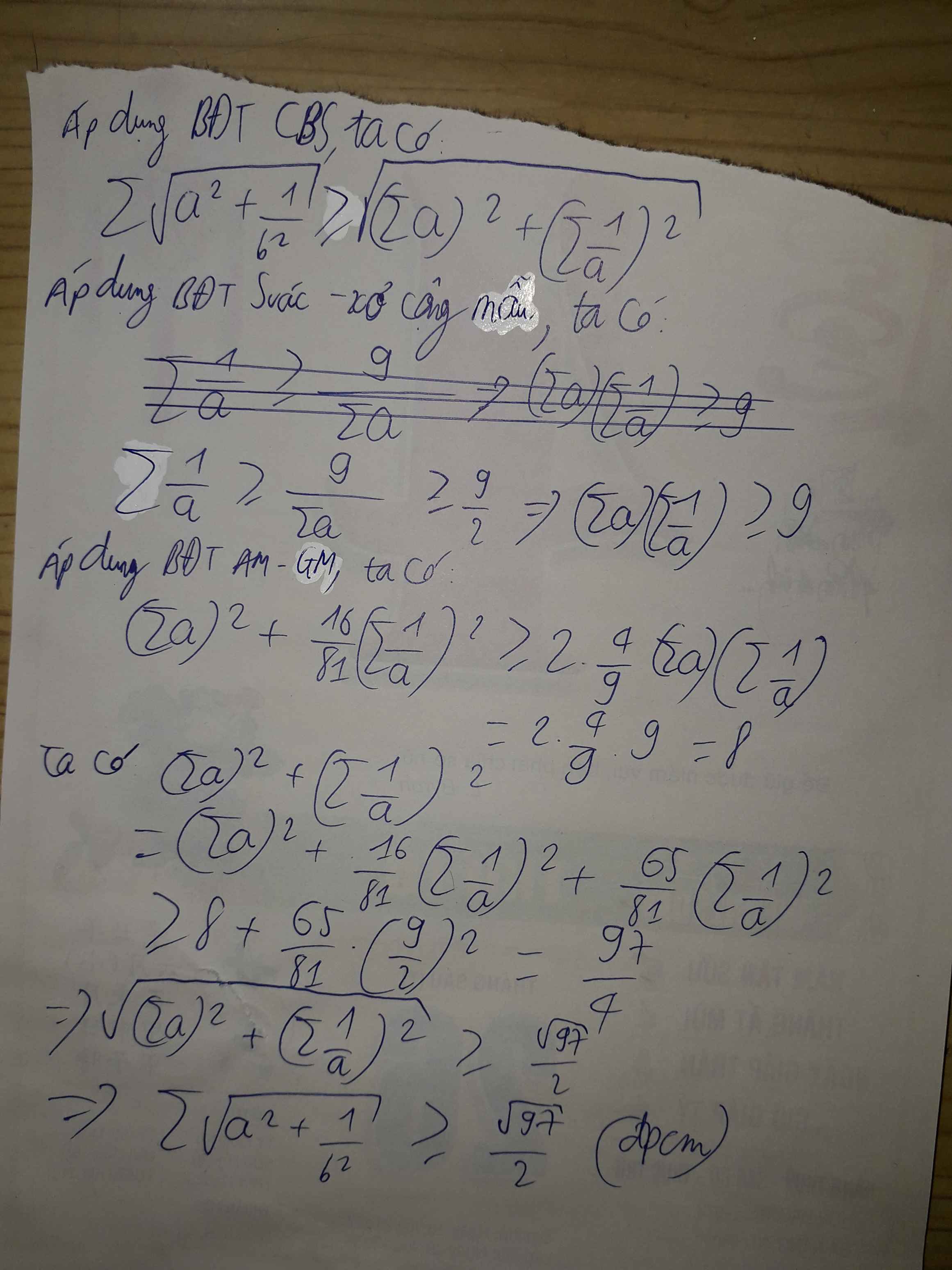
dễ thoy
(1+1+1)!=6
câu dưới mình dg suy nghĩ
BAI NAYTOI CHIU THUA