Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có bảng sau:
| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giữa d, R, r |
|---|---|---|
| (O; R) đựng (O'; r) | 0 | d < R - r |
| Ở ngoài nhau | 0 | d > R + r |
| Tiếp xúc ngoài | 1 | d = R + r |
| Tiếp xúc trong | 1 | d = R – r |
| Cắt nhau | 2 | R – r < d < R + r |

đựng giữa
và giữa
và Tiếp xúc ngoài có 1 điểm chung, giữa
và Tiếp xúc trong có 1 điểm chung, giữa
và cắt nhau có 2 điểm chung, giữa
0; d<R-r
Ở ngoài nhau;0
1;d=R+r
Tiếp xúc trong;1
Cắt nhau;R-r<d<R+r

| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giữa d,R,r |
| (O,R) dựng (O’,r’) | 0 | D<R-r |
| (O;R) ở ngoài nhau (O’;r) | 0 | D>R+r |
| Tiếp xúc ngoài | 1 | D=R+r |
| Tiếp xúc trong | 1 | D=R-r |
| Hai đường tròn cắt nhau | 2 | R-r<d<R+r |

Vị trí tương đối của hai đường tròn (O ; R) và (O’ ; r) (R ≥ r) | Hệ thức giữa OO’ với R và r | Số điểm chung | |
|---|---|---|---|
Hai đường tròn cắt nhau | R – r < OO’ < R + r | 2 | |
Hai đường tròn tiếp xúc nhau | - Tiếp xúc ngoài | OO’ = R + r | 1 |
- Tiếp xúc trong | OO’ = R – r > 0 | ||
Hai đường tròn không giao nhau | - (O) và (O’) ở ngoài nhau | OO’ > R + r | 0 |
- (O) đựng (O’) | OO’ < R - r |
Còn lại phần cuối 0 bên phải nhá Ly yêu?

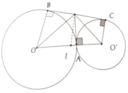
a, Chứng minh được tương tự câu 1a,
=> O ' M O ^ = 90 0
Áp dụng hệ thức lượng trong tam giác vuông tính được MA = R r
b, Chứng minh
S
B
C
O
O
'
=
R
+
r
R
r
c, Chứng minh được: ∆BAC:∆OMO’ => S B A C S O M O ' = B C O O ' 2
=> S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r
d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}

Ta có bảng sau: