Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi cạnh tam giác ABC là x
theo công thức tính diện tích S = p.r với p là nửa chu vi, r là bán kính đường tròn nội tiếp.
Ta có \(\frac{x^2\sqrt{3}}{4}=\frac{3x}{2}.1\Rightarrow x=2\sqrt{3}\) (cm)
Suy ra bán kính đường tròn ngoại tiếp : \(R=\frac{AB.BC.AC}{4.S_{ABC}}\frac{x^3}{\frac{4.x^2\sqrt{3}}{4}}=\frac{x}{\sqrt{3}}=2\) (cm)


Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
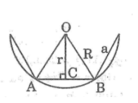
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)
nội tiếp - đường kính-vuông
Chọn B