Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho ΔABC cân tại A có AB=AC=3cm; BC=4cm
BH=1/2BC=1/2x4=2(cm)
Xét ΔABH vuông tại H có \(\cos B=\dfrac{BH}{AB}=\dfrac{2}{3}\)
nên \(\widehat{B}\simeq48^011'\)
=>Góc cần tìm có số đo là \(1^049'\)

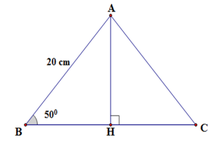
Kẻ AH ⊥ BC tại H. Suy ra H là trung điểm BC (do tam giác ABC cân tại A có AH vừa là đường cao vừa là đường trung tuyến)
Xét tam giác AHB vuông tại H có:
![]()
Mà H là trung điểm của BC nên:

Đáp án cần chọn là: B

Câu 1:
Diện tích tam giác đều cạnh 3cm là:
\(S=\dfrac{3^2\cdot\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{4}\left(cm^2\right)\)
Câu 2:
Nửa chu vi tam giác là:
\(P=\dfrac{C}{2}=\dfrac{8+8+6}{2}=\dfrac{22}{2}=11\left(cm\right)\)
Diện tích tam giác là:
\(S=\sqrt{P\cdot\left(P-A\right)\cdot\left(P-B\right)\cdot\left(P-C\right)}=\sqrt{11\cdot\left(11-8\right)^2\cdot\left(11-6\right)}\)
\(=\sqrt{11\cdot5\cdot9}=3\sqrt{55}\left(cm^2\right)\)
Giả sử tam giác ABC có AB = AC = 3cm, BC = 4cm.
Kẻ AH ⊥ BC. Ta có :
Tam giác ABH vuông tại H nên ta có:
Sai số là: 50 ° - 48 ° 11 ' = 1 ° 49 '