Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
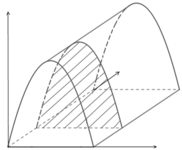
Phương pháp: Sử dụng tích phân.
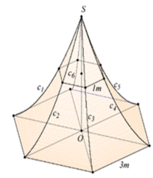
Cách giải: Chọn hệ trục tọa độ như hình sao cho mặt trước của lều là mặt (Oxy), mặt đáy lều là mặt (Oyz).
Chi phí dán hoa văn là 200.000 đồng cho một
m
2
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?
Đáp án C
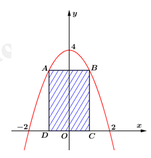Gọi S là diện tích hình phẳng giới hạn bởi Parabol có phương trình
y
=
4
-
x
2
và trục hoành
Suy ra ∫ - 2 2 4 - x 2 d x = 32 3 m 2
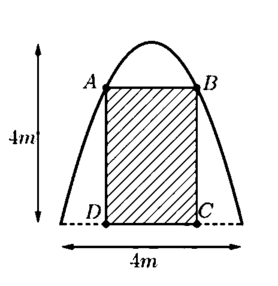
Gọi điểm C a ; 0 , a > 0 ⇒ D - a ; 0 B ( a ; 4 - a 2 ) , A - a ; 4 - a 2
Gọi S 1 là diện tích ABCD, suy ra S 1 = A B . B C = 2 a . 4 - a 2 m 2
Gọi S 2 là diện tích có hoa văn, suy ra S 2 = S - S 1
S 2 nhỏ nhất khi và chỉ khi S 1 lớn nhất
Xét hàm số f a = 2 a 4 - a 2 , a ∈ 0 ; 4
Ta có f ' a = 8 - 6 a 2 ⇒ f ' a = 0 ⇔ a = 2 3
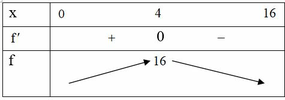
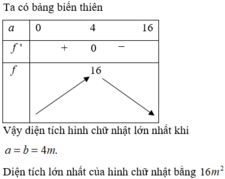
Xét bảng biến thiên hàm số f(a) với a ∈ 0 ; 4
Suy ra m a x 0 ; 4 f a = f 2 3 = 32 3 9 m 2 . Suy ra S 2 m i n = 32 3 - 32 3 9 ≈ 4 , 51 m 2
Suy ra số tiền cần bằng 902.000 đồng.
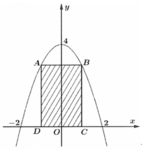
Chọn hệ trục tọa độ như hình vẽ. Khi đó phương trình Parabol có dạng:
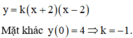
Gọi là diện tích hình phẳng giới hạn bởi Parabol có phương trình y = 4 - x 2 và trục hoành.
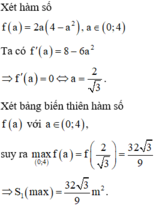
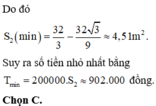
Đáp án B.
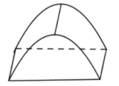
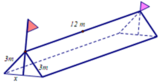
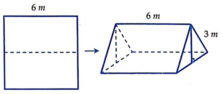
Không gian lều là một khối lăng trụ đứng có chiều cao là 6 m, đáy là tam giác cân có cạnh bên là 3 m và góc ở đỉnh là φ ∈ 0 ; 180 ° .
Khi đó thể tích của khối lăng trụ là: V = 1 3 . 1 2 . 3 . 3 sin φ . 6 = 9 sin φ ( m 3 )
⇒ V m a x ⇔ sin φ m a x ⇒ φ = 90 °
Gọi chiều cao gậy là h ⇒ h = 3 2 2 (m)
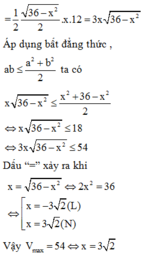
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Gọi phương trình parabol là: y = a x 2 + b x + c