Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của canô là x (km/h,x > 6)
vận tốc canô khi xuôi dòng là :x + 6(km/h)
vận tốc canô khi ngược dòng là: x - 6(km/h)
thời gian canô xuôi dòng: 36/(x + 6)(giờ)
thời gian canô ngược dòng: 36/(x - 6)(giờ)
VÌ thời gian cả đi và về là 4,5 giờ nên ta có phương trình:
36/(x + 6) + 36/(x - 6) = 4,5
4,5x^2 - 72x - 162 = 0
=> x= 18
Vậy vận tốc của ca nô là 18km/h
=> vận tốc canô khi xuôi dòng là 18+6=24(km/h)

Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\Rightarrow x=18\)
Vậy ...

Bài 2: a,b thế số vào rồi giải
c) x = -2 là nghiệm của pt
=> 4.(-2)^2 - 25 + k^2 + 4k.(-2) = 0
Từ đó giải ra tìm k và kết luận.

Thời gian đi từ A đến B là 11h30p-7h=3h30p
Đổi 3h30p=3,5h
Gọi thời gian xuôi dòng từ A đến B là: x(giờ)(ĐK x>0)
Thời gian từ B về A là: 3,5-x(giờ)
Vận tốc xuôi dòng là: (36/x)+6(km/h)
Vận tốc ngược dòng là: (36/3,5-x)-6(km/h)
Vì quãng đường AB ko đổi nên ta có phương trình
(36/x)+6-(36/3,5-x)-6=6
rồi giải tiếp nha !!

Lời giải:
Tổng thời gian đi lẫn về là: $11h30-7=4h30=4,5$h
Gọi thời gian đi là $x$ (h) thì thời gian về là $4,5-x$ (h)
Vận tốc cano xuôi dòng: $\frac{AB}{x}=\frac{36}{x}$
Vận tốc cano ngược dòng: $\frac{AB}{4,5-x}=\frac{36}{4,5-x}$
Chênh lệch vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước, tức là:
$\frac{36}{x}-\frac{36}{4,5-x}=12$
$\Leftrightarrow \frac{3}{x}-\frac{3}{4,5-x}=1$
$\Rightarrow x^2-10,5x+13,5=0$
$\Rightarrow x=9$ hoặc $x=1,5$. Hiển nhiên $x< 4,5$ nên $x=1,5$
Vận tốc cano xuôi dòng là: $\frac{36}{1,5}=24$ (km/h)

Gọi x (km/h) là vận tốc thực của ca nô. Điều kiện: x > 6
Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)
Vận tốc của ca nô khi ngược dòng là x – 6 (km/h)
Thời gian lúc ca nô đi xuôi dòng là 36/(x + 6) (giờ)
Thời gian lúc ca nô đi ngược dòng là 36/(x - 6) (giờ)
Thời gian ca nô đi và về:
11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = 9/2 giờ
Theo đề bài, ta có phương trình:
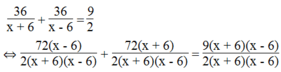
⇔ 72(x – 6) + 72(x + 6) = 9(x + 6)(x – 6)
⇔ 72x – 432 + 72x + 432 = 9x2 – 324
⇔ 9x2 – 144x – 324 = 0
⇔ x2 – 16x – 36 = 0
⇔ x2 + 2x – 18x – 36 = 0
⇔ x(x + 2) – 18(x + 2) = 0
⇔ (x + 2)(x – 18) = 0
⇔ x + 2 = 0 hoặc x – 18 = 0
x + 2 = 0 ⇔ x = -2 (loại)
x – 18 = 0 ⇔ x = 18 (thỏa)
Vậy vận tốc thực của ca nô là 18km/h, suy ra vận tốc của ca nô lúc xuôi dòng là 18 + 6 = 24 (km/h).

gọi vận tốc của canô là x (x > 6)
vận tốc canô khi xuôi dòng là x + 6
vận tốc canô khi ngược dòng là x - 6
thời gian canô xuôi dòng: 36/(x + 6)
thời gian canô ngược dòng: 36/(x - 6)
thời gian cả đi và về là 4,5 giờ:
=> 36/(x + 6) + 36/(x - 6) = 4,5
4,5x^2 - 72x - 162 = 0
=> x= 18
=> vận tốc canô khi xuôi dòng là 24km/h
Gọi Vận tốc xuôi dòng ca nô là \(x\) ( đk : \(x>6\))
VẬn tộc ngược dòng là :
\(x-6\)
Zận tốc xuôi dòng \(x+6\)
Thời gian đi từu A - B đi xuôi dòng nước là : \(\frac{36}{x+6}\)
Thời gian đi từ A - B đi ngược dòng nước là \(\frac{36}{x-6}\)
Thời gian ca nô đì từ A - B rồi quay từ B về A là
\(11h30-7h=4,5h\)
Theo bài ra ta có pt:
\(\frac{36}{x+6}+\frac{36}{x-6}=4,5=>x=18\)

a) Xét hình chữ nhật ABCD có:
AB//CD => \(\widehat{ABH}=\widehat{BDC}\) (2 góc so le trong)
Xét tam giác AHB và tam giác BCD có:
\(\widehat{ABH}=\widehat{BDC}\left(cmt\right)\)
\(\widehat{AHB}=\widehat{BCD}=90^0\)
=> \(\Delta AHB\sim\Delta BCD\left(g.g\right)\)
b) Xét tam giác ADH và tam giác BDA có:
\(\widehat{ADB}\) chung
\(\widehat{AHD}=\widehat{BAD}=90^0\)
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DH}=\dfrac{DB}{AD}\Rightarrow AD^2=DH.DB\)
c) Xét tam giác BDC vuông tại C có:
\(BD^2=BC^2+DC^2\) (Định lý Pytago)\(\Rightarrow BD=\sqrt{BC^2+CD^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có: \(AD^2=DH.DB\left(cmt\right)\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Xét tam giác ADH vuông tại H có:
\(AD^2=AH^2+DH^2\)( định lý Pytago)
\(\Rightarrow AH=\sqrt{AD^2-DH^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

Gọi vận tốc thực của ca nô là x (km/h)(x>0)Đổi: 11h30p = 11,5hVận tốc lúc xuôi dòng của ca nô là: x+6 (km/h)Vận tốc lúc ngược dòng của ca nô là: x-6 (km/h)Tổng thời gian cả đi lẫn về của ca nô là: 11,5 - 7 = 4,5 (giờ)Thời gian đi từ A xuôi dòng đến B là: 36/x+6 (giờ)Thời gian đi từ B ngược dòng về A là: 36/x-6 (giờ)Vì tổng thời gian cả đi lẫn về của ca nô là 4,5 (giờ) nên ta có phương trình:36/(x+6) + 36/(x-6) = 4,5<=> 36(x-6)/(x+6)(x-6) + 36(x+6)/(X+6)(x-6) = 4,5(x+6)(x-6)/(x+6)(x-6)=> 36x - 216 + 36x + 216 = 4,5x^2 - 162<=> 72x - 4,5x^2 + 162 = 0<=> 81(x + 2) - 4,5x(x + 2) = 0<=> (81 - 4,5x)(x + 2) = 0Vậy: 81 - 4,5x = 0 hoặc x + 2 = 0 <=> x = 18(nhận) <=> x = -2(loại) Suy ra vận tốc thực của ca nô là 18 (km/h)Vậy vận tốc của ca nô khi xuôi dòng là: x + 6 = 18 + 6 = 24 (km/h)

Gọi vận tốc cano khi xuôi dòng là x + 6 ( x > 6 )
Vận tốc ngược dòng là x - 6
Tgian đi xuôi dòng là \(\dfrac{36}{x+6}\)
Tgian về ngược dòng là \(\dfrac{36}{x-6}\)
Tổng tgian từ lúc đi --> bến B
\(=12h30p-8h=4h30p=4,5h\)
Vì tổng tgian từ lúc đi --> bến B là 4,5h nên ta có pt
\(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\left(4,5h\right)\)
Giải pt trên ta đc\(\Rightarrow x=18+6=24km\)
Bài 1:
a: Ta có: 4x+20=0
nên 4x=-20
hay x=-5
b: Ta có: \(\left(x^2-2x+1\right)-4=0\)
\(\Leftrightarrow\left(x-1\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
c: Ta có: \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x+1\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}\)
Suy ra: \(x^2+3x+x^2-2x+x-2=2x^2+2x\)
\(\Leftrightarrow4x-2-2x=0\)
\(\Leftrightarrow2x=2\)
hay \(x=1\left(nhận\right)\)
Bài 2:
Ta có: \(3x-\left(7x+2\right)>5x+4\)
\(\Leftrightarrow3x-7x-2-5x-4>0\)
\(\Leftrightarrow-9x>6\)
hay \(x< -\dfrac{2}{3}\)