Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có n = R 2 R 1 = 4 → P = n n + 1 2 P max ⇒ P m a x = 125 W
Đáp án A

Đáp án B
Khi C=C0 , Pmax= 60W, khi đó Zc0= ZL , và Pmax= U 2 R =60
Khi C= 2C0, thì Zc= ½ ZC0 và Pmax = U 2 R 2 + 1 4 Z C 0 2 R =48
=> ZC0 = R
Khi C=1,5 C0 , ZC= 2/3 ZC0 => P= U 2 R 2 + 2 3 Z C 0 - Z L 2 R = 9U2/10R= 54(W)

Đáp án B
Khi C=
C
0
,
P
m
a
x
= 60W, khi đó
Z
C
0
=
Z
L
, và ![]()
Khi C= 2 C 0 , thì Z C = 1 / 2 Z C 0 và Pmax =48
=> Z C 0 = R
Khi C=1,5 C 0 , Z C = 2 / 3 Z C 0 => P= 54(W)

Đáp án D
R thay đổi, công suất bằng nhau nên có công thức R 1 R 2 = ( Z L − Z C ) 2
Khi R = R1 = 15Ω : P = U 2 R 1 Z 1 2 = U 2 R 1 R 1 2 + R 1 R 2 = U 2 R 1 + R 2 (1)
Khi R = R0 : P m ax = U 2 2 R 0 R 0 = Z L − Z C ⇒ R 0 = 30 ( Ω ) (2)
Từ (1) và (2) suy ra P m ax P = R 1 + R 2 2 R 0 ⇒ P m ax = 375 ( W )

Đáp án D
R thay đổi, công suất bằng nhau nên có công thức ![]()
Khi R = R1 = 15Ω 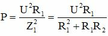 (1)
(1)
Khi R = R0 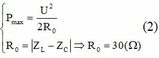
Từ (1) và (2) suy ra