Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.17. Đặt hai gương phẳng vuông góc với nhau chiếu một tia sáng SI bất kỳ vào gương G1 có góc tới i = 300. Tia phản xạ cuối cùng qua G2 có phương như thế nào đối với tia tới SI? Vuông góc với SI.
A. Song song với SI.
B. Có phương cắt tia SI
C. Hợp với SI 300.
D. Hợp với SI 600.

a, Đầu tiên vẽ tia tới chiếu đến gương G1 tại I, rồi phản đến gương G2 tại điểm I' , rồi phản xạ tiếp qua điểm R
b, Ta có tia pháp tuyến \(NI\perp I\) (G1) , \(NI'\perp I'\left(G2\right)\)
mà 2 gương G1 , G2 vuông góc vói nhau
\(\Rightarrow\left\{{}\begin{matrix}i=90^o-45^o=45^o\\i=i'\Leftrightarrow i'=45^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}i2=90^o-45^o=45^o\\i2=i2'\Leftrightarrow i2'=45^o\end{matrix}\right.\)
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 : \(45^o+45^o+45^o+45^o=180^o\)
Tham khảo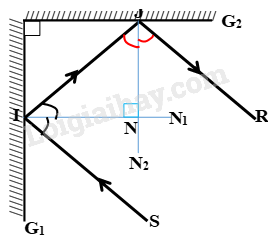
Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1IN1 và JN2JN2 cũng vuông góc với nhau.
Định luật phản xạ tại gương G1G1:
ˆSIN=ˆNIJ⇒ˆSIJ=2ˆNIJ(1)SIN^=NIJ^⇒SIJ^=2NIJ^(1)
Định luật phản xạ tại gương G2G2:
ˆIJN=ˆNJR⇒ˆIJR=2ˆIJN(2)IJN^=NJR^⇒IJR^=2IJN^(2)
ΔIJNΔIJN vuông tại NN:
ˆNIJ+ˆNJI=900NIJ^+NJI^=900
⇒ˆSIJ+ˆIJR=2ˆNIJ+2ˆNJI=2(ˆNIJ+ˆNJI)=1800⇒SIJ^+IJR^=2NIJ^+2NJI^=2(NIJ^+NJI^)=1800
Vậy tia tới SISI song song với tia phản xạ JRJR. Góc tạo bởi tia tới SISI và tia phản xạ cuối cùng trên gương G2G2 có giá trị 1800

Để bik thêm chi tiết, xin zui lòng lật sách BTVL7, trg 14, câu 4.11
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 có giá trị là 0o.
Vậy chọn A.
Có 2 cách để vẽ:
Cách 1:
+ Vẽ tia phản xạ tại I, tia này gặp gương G2 tại J.
+ Tại J vẽ tia phản xạ.
Cách 2:
+ Vẽ ảnh S1 của S qua gương G1
+ Vẽ ảnh S2 của S1 qua gương G2
+ Tia phản xạ tại I có đường kéo dài đi qua S1, đến gặp G2 tại J
+ Tia phản xạ tại J có đường kéo dài đi qua S2.