Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng kết quả bài toán: Mạch RLC khi R=R1 hoặc R=R2 thì công suất tiêu thụ trên đoạn mạch như nhau, khi đó:
\(R_1R_2=Z_C^2\)
\(\Rightarrow8R_1^2=Z_C^2\)
\(\Rightarrow Z_C=2\sqrt{2}R_1\)
Khi đó:
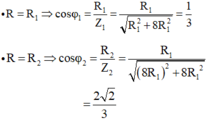
+ R=R1 thì \(\cos\varphi_1=\frac{R_1}{Z_1}=\frac{R_1}{\sqrt{R_1^2+8R_1^2}}=\frac{1}{3}\)
+ R = R2 thì \(\cos\varphi_2=\frac{R_2}{Z_2}=\frac{8R_1}{\sqrt{\left(8R_1\right)^2+8R_1^2}}=\frac{2\sqrt{2}}{3}\)
Chọn C.

- Khi R = R1 hoặc R = R2 thì công suất tiêu thụ trên đoạn mạch như nhau, suy ra:
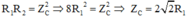
- Do vậy:

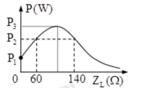
- Từ đồ thị ta thấy có hai giá trị của ZL là 60Ω và 140Ω cùng cho 1 giá trị P.
- Vị trí P3 đạt cực đại ứng với trường hợp cộng hưởng điện ZL = ZC
- Và có mối quan hệ giữa ZL3 với ZL1 và ZL2 là:
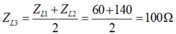
- Khi ZL = 0 thì mạch có công suất P1 thỏa mãn P3 /P1 = 3. Ta có:
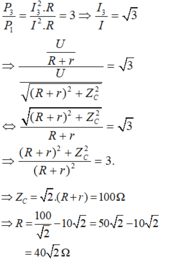

Đáp án C
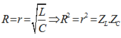
Đặt ZL = 1 và ZC = x => R2 = r2 = x
Vì theo đề bài: UMB = n.UAM => ZMB = nZAM
![]()

Hệ số công suất của mạch: 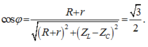

Giá trị của biến trở để công suất tiêu tụ trên toàn mạch cực đại R 0 = Z L − Z C − r = 80 Ω.
→ Công suất của mạch khi đó P = U 2 2 R + r = 144 W.
Đáp án D



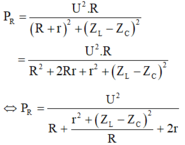
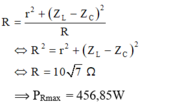
Hai giá trị của R cho cùng công suất tiêu thụ trên mạch thõa mãn R 1 R 2 = R 0 2 = Z L − Z C 2
→ Hệ số công suất
cos φ = R R 2 + Z L − Z C 2 ⇒ cos φ 1 = R 1 R 1 2 + R 1 R 2 = 1 3 cos φ 1 = R 2 R 2 2 + R 1 R 2 = 2 2 3
Đáp án A