Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
I01 = I02 = > Z1 = Z2 =>
Z
L
=
2
Z
C
tan φ1 =
Z
L
-
Z
C
R
=
Z
C
R
tan φ2 =
-
Z
C
R
=> tan φ1 = - tan φ2 = > φ1 = -φ2
=> φu - φi1= -(φu - φi2) => φu =
π
12
=> u = 60 2 cos(100πt + π 12 ) V

Chọn C
I01 = I02 = > Z1 = Z2 =>
Z
L
=
2
Z
C
tan
φ
1
=
Z
L
-
Z
C
R
=
Z
C
R
tan
φ
2
=
-
Z
C
R
=> tan φ1 = - tan φ2 = > φ1 = -φ2
=> φu - φi1= -(φu - φi2) => φu =
π
12
=> u = 60 2 cos(100πt + π 12 ) V

+ Vì I1 = I2 → Z1 = Z2 → φ1 = φ2.
→ Đáp án C là thõa mãn.
Đáp án C

Giải thích: Đáp án C
+ Từ biểu thức của i1 và i2 ta có: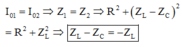
+ Độ lệch pha giữa điện áp và cường độ dòng điện khi chưa ngắt tụ điện sau khi ngắt tụ điện:
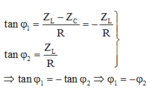
+ Ta lại có: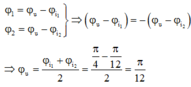
+ Biểu thức của điện áp giữa hai đầu đoạn mạch: 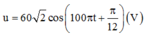

Đáp án A
Trong 2 trường hợp thì cường độ dòng điện cực đại có giá trị là như nhau


Đáp án D
Cách giải:
Theo đề

Mặt khác 
Từ (2), (3) ![]()
Khi RLC nt
→
cộng hưởng: 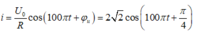

Giải thích: Đáp án D
+ Từ phương trình i1 và i2 ta thấy: ![]()

+ Độ lệch pha của mạch trong hai trường hợp:
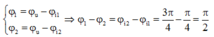
+ Hai góc lệch pha nhau
π
2
nên: ![]()

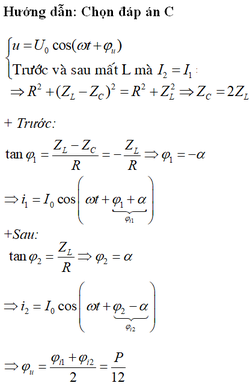
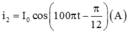
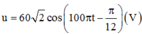
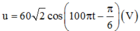
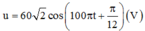
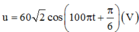
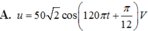
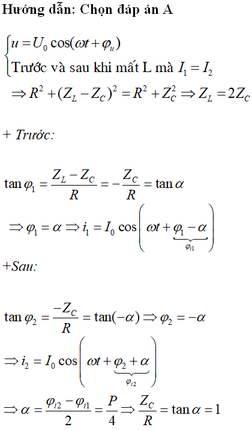
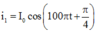
Do giá trị hiệu dụng I1 = I2
nên Z1 = Z2
Ta có thể biểu diễn Z trên giản đồ như thế này.
Chiều của Z chính là chiều của điện áp u
+ So với i1 thì pha ban đầu của u là: \(\frac{\pi}{4}-\alpha\)
+ So với i2 thì pha ban đầu của u là: \(-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\frac{\pi}{4}-\alpha=-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\alpha=\frac{\pi}{6}\)
\(\Rightarrow\varphi_u=\frac{\pi}{4}-\frac{\pi}{6}=\frac{\pi}{12}\)
Vậy \(u=60\sqrt{2}\cos\left(100\pi t+\frac{\pi}{12}\right)V\)