Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chuẩn hóa ω 1 = 1 ⇒ ω 2 = 4 3
Ta có ω C ω L = 1 − R 2 C 2 L = 1 − R 2 2 L 2 1 ω 1 ω 2 ⇒ R 2 L 2 = 2 3
Điện áp hiệu dụng cực đại giữa hai đầu cuộn cảm khi ω = ω 2 = 4 3
: U L m a x = U 1 − ω 1 ω 2 2 ⇒ U = 220 V
Giá trị cực đại của điện áp hiệu dụng trên tụ điện khi C thay đổi: U C m a x = U 1 + L 2 R 2 ω 2 2 = 421 V
Đáp án C

Đáp án C
+ Áp dụng kết quả chuẩn hóa của bài toán ω biến thiên
=> hệ số
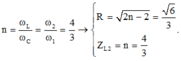
+ Điện áp cực đại trên cuộn dây khi biến thiên
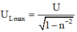
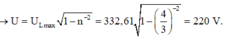
+ Điện áp cực đại trên tụ điện khi C biến thiên
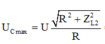
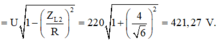
Ghi chú:
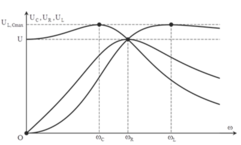
Ta để ý rằng khi tăng dần ω thì thứ tự cực đại của các điện áp là ω C = X L → ω L = 1 L C
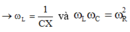
+ Để đơn giản cho biểu thức ta tiến hành chuẩn hóa X = 1 và n = ω L ω C = L C
Khi U C m a x thì
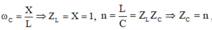
Khi đó:
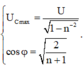
Khi U L m a x thì
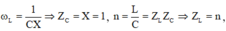
Khi đó:
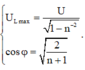

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
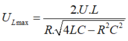
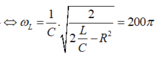
Và điện áp trên tụ cực đại là:
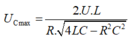
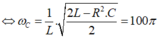
Dễ thấy:
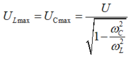
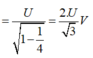

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
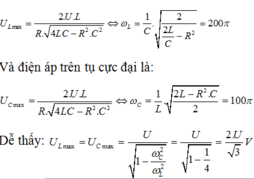

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + n
Mặc khác U U L m a x 2 + 1 n 2 = 1 → ω L ω C = 2 3
→ Vậy cos φ = 2 1 + n = 0 , 96
Đáp án D

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + ω L ω C
Mặc khác U U L m a x 2 + ω C ω L 2 = 1 ⇒ ω C ω L = 3 2
→ Vậy cos φ = 2 1 + ω L ω C = 0 , 96
Đáp án D
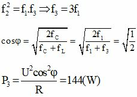
Ta có n = ω L ω C = 4 3 ω 1 ω 1 = 4 3 .
→ U L m a x = U 1 − n − 2 → U = U L m a x 1 − n − 2 = 220 V.
Điện áp hiệu dụng cực đại ở hai đầu tụ điện khi thay đổi C:
U C m a x = U R 2 + Z L 2 2 R = U 1 + Z L 2 2 R 2 = U 1 + n 2 2 n − 2 = 220 1 + 4 3 2 2 4 3 − 2 = 421 , 27 V
ü Đáp án C