Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương pháp: Sử dụng công thức
Cách giải: Ta có:
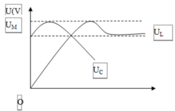
Từ đồ thị, ta thấy:
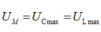
Xét:
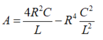
Mặt khác, ta có:
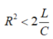
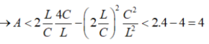
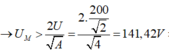
=>Chọn B
Cách giải: Đáp án A
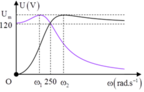
Khi ω = 0 thì UC = U, khi
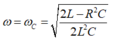
thì U C cực đại
Khi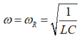 
thì
U
R
đạt cực đại bằng U
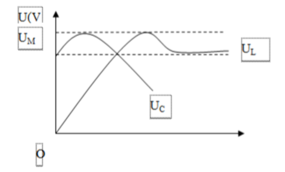
Khi ω = 0 thì U L = 0
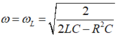Khi 
thì 
Đặt
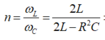
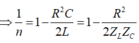
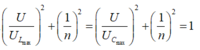
Tại giao điểm của hai đồ thị, ta có U L = U C = U (cộng hưởng)
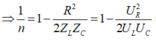
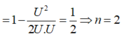
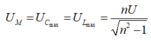
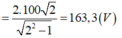
Đáp án B
Khi ω biến thiên:
Mặt khác giá trị ω để UL = UAB nhỏ hơn giá trị ω để ULmax 2 lần
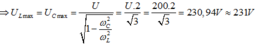
Đáp án C
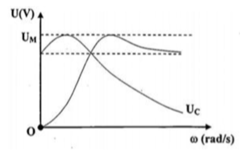
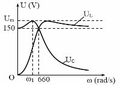
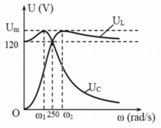
Từ đồ thị ta thấy:
+
ω
= 0 thì 
+
ω
=
ω
0
=
660
thì 
TH này có cộng hưởng điện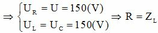 
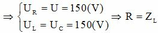
ω = ω 1 thì U C max.
Các công thức:
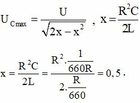
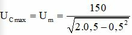
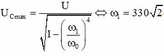
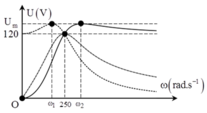
Từ hình vẽ ta thấy rằng 250 = 2 ω C 250 = ω L 2 ⇒ n = ω L ω C = 2 ⇒ cos φ = 2 1 + n = 2 3
Đáp án C
Từ hình vẽ ta thấy rằng 250 = 2 ω C 250 = ω L 2
→ n = ω L ω C = 2 → cos φ = 2 1 + n = 2 3
Đáp án C
Đáp án C
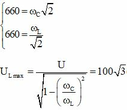
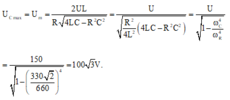
Ta có ngay U = 150 (V) ( ω = 0 thì U C = U)
Gọi ω C là giá trị để U C max, ω L là giá trị để U C max. Ta có
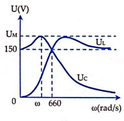
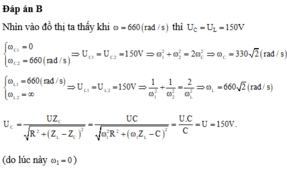
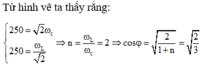
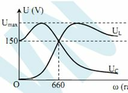
Đáp án B
Phương pháp: từ đồ thị và sử dụng các công thức về điều kiện cực đại khi ω biến thiên
Cách giải: Khi ω biến thiên
Từ đồ thị ta nhận thấy:
.Khi ω2 = 0 thì ZC =∞ => I= 0A; UL =0V Khi ω2 =ωL2 thì ULmax.
Khi ω2 = ∞ thì ZL = ∞; UL = UAB. Tương tự với UC. Mặt khác giá trị ω để UL = UAB nhỏ hơn giá trị ω để ULmax 2 lần
Ta có: