Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đáp án C
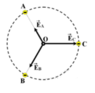
E = k Q r 2 ⇒ E A = k q r 2 = E 0 E B = k 2 q r 2 = 2 E 0 E C = k 4 q r 2 = 4 E 0
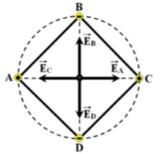
+ Từ E → = E → A + E → B + E → C
vì không có tính đối xứng nên ta có thể tổng hợp theo phương pháp số phức (chọn véc tơ làm chuẩn)
E ¯ = E A ∠ 120 0 + E B ∠ - 120 0 + E C
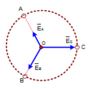
E ¯ = E 0 ∠ 120 0 + 2 E 0 ∠ - 120 0 + 4 E 0 = 7 E 0 ∠ - 19 0 ⇒ E = 7 k q r 2 = 3 7 k q a 2

Đáp án C
![]()
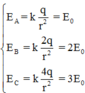
Từ
![]()
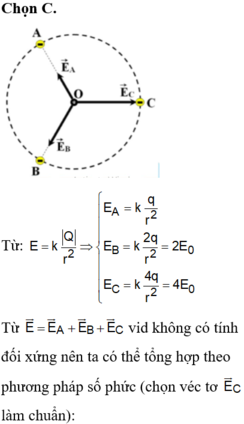
vì không có tính đối xứng nên ta có thể tổng hợp theo phương pháp số phức (chọn véc tơ E C → làm chuẩn)
![]()
![]()
![]()
![]()

đáp án C
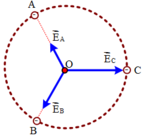
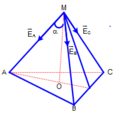
E = k Q r 2 ⇒ E A = E B = E C = k q x 2 + a 2
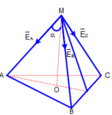
+ Vì ba véc tơ E → A , E → B , E → C nhận MO là trục đối xứng nên véc tơ tổng hợp E → = E → A + E → B + E → C nằm trên MO và có độ lớn
E = E A cos α + E B cos α + E C cos α
= 3 k q x 2 + a 2 x x 2 + a 2 = 0 , 375 . k q a 2

Đáp án C
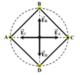
E = k Q r 2 ⇒ E A = E B = E C = k q x 2 + a 2
Vì ba véc tơ E → A , E → B , E → C nhận MO là trực đối xứng nên tổng hợp
E → = E → A + E → B + E → C nằm trên MO và có độ lớn
E = E A cos α + E B cos α + E C cos α
= 3 k q x 2 + a 2 x x 2 + a 2 = 0 , 375 . k q a 2


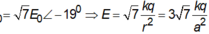


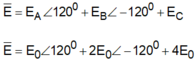
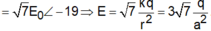
Đáp án C
E = k Q r 2 ⇒ E A = k q r 2 = E 0 E B = k 2 q r 2 = 2 E 0 E C = k 4 q r 2 = 4 E 0
Từ E → = E → A + E → B + E → C vì không có tính đối xứng nên ta có thể tổng hợp theo phương pháp số phức (chọn véc tơ làm chuẩn)
E ¯ = E A ∠ 120 0 + E B ∠ - 120 0 + E C
E ¯ = E 0 ∠ 120 0 + 2 E 0 ∠ - 120 0 + 4 E 0 = 7 E 0 ∠ - 19 0 ⇒ E = 7 k q r 2 = 3 7 k q a 2