Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(f\left(x\right)=-x^4+3x^3-\frac{1}{3}x^2+2x+5\)
\(g\left(x\right)=x^4+3x^3-\frac{2}{3}x^2-2x-10\)
b) \(f\left(x\right)+g\left(x\right)=-x^4+3x^3-\frac{1}{3}x^2+2x+5+x^4+3x^3-\frac{2}{3}x^2-2x-10\)
\(=6x^3-x^2-5\)
c) +) Thay x=1 vào đa thức f(x) + g(x) ta được :
\(6.1^3-1^2-5=0\)
Vậy x=1 là nghiệm của đa thức f(x) + g(x)
+) Thay x=-1 vào đa thức f(x) + g(x) ta được :
\(6.\left(-1\right)^3-\left(-1\right)^2-5=-10\)
Vậy x=-1 ko là nghiệm của đa thức f(x) + g(x)

a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.

\(f\left(x\right)=\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-1=0\\x-3=0\end{cases}}\Rightarrow\hept{\begin{cases}x-1\\x-3\end{cases}}\)
=> x = 1 và x = 3 là nghiệm của đa thức f(x)
Mà nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x)
=> nghiệm của đa thức g(x) là x = { 1; 3 }
Với x = 1 thì \(g\left(x\right)=1^3-a.1^2+b.1-3=0\)
\(\Rightarrow-a+b=2\)(1)
Với x = 3 thì \(g\left(x\right)=3^3-a.3^2+3b-3=0\)
\(\Rightarrow3a-b=8\)(2)
Cộng vế với vế của (1) và (2) ta được : ( - a + b ) + (3a - b) = 10
=> 2a = 10 => a = 5
=> - 5 + b = 2 => b = 7
Vậy a = 5 ; b = 7
(x-1)(x-3)=0
=>x-1=0 hoặc x-3=0
=>x=1 hoặc x=3
Vậy nghiệm của f(x) là 1 và 3
Nghiệm của g(x) cũng là 1 và 3
Với x=1 ta có g(x)=1+a+b-3=0
=>a+b-2=0
a+b=2
Với x=3 ta có g(x)=27-9a+3b-3=0
=>24-9a+3b=0
=>8-3a+b=0
=>3a-b=8
a=\(\frac{8+b}{3}\)
Vậy với a+b=2 hoặc \(a=\frac{8+a}{3}\) thì nghiệm của đa thức f(x) cũng là nghiệm của g(x)

\(a=\frac{6.2.3.4+6.3.4.5+6.4.5.6+...+6.98.99.100}{2.3.4+3.4.5+4.5.6+...+98.99.100}=6\)
thay vào p(x) suy ra a không là nghiệm của đa thức nhé bạn

Vì đa thức g(x) là đa thức bậc 3 và mọi nghiệm của f(x) cũng là của g(x) nên:
G/s \(g\left(x\right)=\left(x-1\right)\left(x+3\right)\left(x-c\right)\) \(\left(c\inℝ\right)\)
Khi đó: \(x^3-ax^2+bx-3=\left(x-1\right)\left(x+3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=\left(x^2+2x-3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=x^3-\left(c-2\right)x^2-\left(2c+3\right)x+3c\)
Đồng nhất hệ số ta được:
\(\hept{\begin{cases}a=c-2\\b=-2c-3\\c=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-3\\b=-1\\c=-1\end{cases}}\)
Vậy a = -3 , b = -1

Vì \(P\left(x\right)=Q\left(x\right)+Q\left(1-x\right)\)
+)\(x=0\) \(\implies\) \(P\left(0\right)=Q\left(0\right)+Q\left(1\right)=0\)
+)\(x=1\) \(\implies\) \(P\left(1\right)=Q\left(1\right)+Q\left(0\right)\)
\(\implies\) \(P\left(0\right)=P\left(1\right)=0\)
Đặt đa thức : P(x) = an . \(x^n\) + an - 1 . \(x^{n-1}\) + ...... + a1 . \(x^1\) + a0
P(x) là đa thức bậc n ; có các hệ số là : an ; an - 1; .... ; a1 ; a0
P(1) = an + an - 1 + ......... + a1 + a0 = 0
Mà a0 ; a1 ; ..... ; an - 1 ; an \(\geq\) 0
\(\implies\) an + an - 1 + ... + a1 + a0 \(\geq\) 0
\(\implies\) P(x) \(\geq\) 0
Dấu " = " xảy ra \(\iff\) a0 = a1 = ..... = an - 1 = an = 0
\(\implies\) P(x) = 0 với mọi x \(\in\) R
\(\implies\) P(7) = 0
\(\implies\) P(P(7)) = P(0) = 0
Vậy P(P(7)) = 0
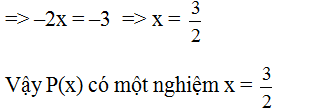
Đa thức là các tổng ( hiệu ) của các đơn thức
lý dó \(\left(x+1\right)\left(x+3\right)\) là đa thức vì nó bằng \(x^2+4x+3\) là tổng của 3 đơn thức
-Đa thức là một đơn thức hoặc một tổng của hai hay nhiều đơn thức
-Vì (x+1) (x+3) có 1 tổng của 2 đơn thức
Mik cx ko chắc lám đâu nha nếu sai bn thông cảm nha