Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=180^0-\left(A+B\right)=75^0\)
Áp dụng định lý hàm sin:
\(\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow c=\dfrac{b.sinC}{sinB}=\dfrac{8.sin75^0}{sin45^0}=4+4\sqrt{3}\)

2 . \(\frac{3}{7}\) + (\(\frac{2}{9}\) . 1\(\frac{3}{7}\) ) - \(\frac{5}{3}\) : \(\frac{1}{9}\)
= \(\frac{6}{7}\) + (\(\frac{2}{9}\) . \(\frac{10}{7}\) ) -\(\frac{5}{3}\) . 9
=\(\frac{6}{7}\) +\(\frac{20}{63}\) - 15 = \(\frac{74}{63}\) -15 = \(\frac{-871}{63}\)
 nó có đẹp ko
nó có đẹp ko

Gọi G là trọng tâm tam giác\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Đặt \(P=MA^2+MB^2+MC^2=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3MG^2+GA^2+GB^2+GC^2\)
Do \(GA^2+GB^2+GC^2\) ko đổi nên \(P_{min}\) khi \(MG_{min}\Leftrightarrow M\) là chân đường vuông góc hạ từ G xuống BC
\(\Rightarrow\dfrac{CM}{BC}=\dfrac{2}{3}\Rightarrow\dfrac{BM}{BC}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{1}{3}\)

CHỌN C vì :
Hệ số góc của đường thẳng d có vectơ chỉ phương u→ = (-1; \(\sqrt{3}\)) là:

\(5x-1>2x+3\)
\(\Leftrightarrow5x-2x>3+1\)
\(\Leftrightarrow3x>4\)
\(\Leftrightarrow x>\dfrac{4}{3}\)
--> Chọn C
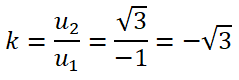
\(D=\dfrac{3}{18\cdot21}+\dfrac{3}{21\cdot24}+\dfrac{3}{24\cdot27}+...+\dfrac{3}{123\cdot126}\\ =\dfrac{1}{18}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{24}+\dfrac{1}{24}-\dfrac{1}{27}+...+\dfrac{1}{123}-\dfrac{1}{126}\\ =\dfrac{1}{18}-\dfrac{1}{126}\\ =\dfrac{1}{21}\)