cứu tui câu C vớiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 3 2022
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1
9 tháng 2 2020
\(\left\{{}\begin{matrix}x-y=1\left(1\right)\\\left(m+1\right)x+my=m+2\left(2\right)\end{matrix}\right.\) từ (1) ta được: \(y=x-1\) Thay vào (2) ta được: \(\left(m+1\right)x+m\left(x-1\right)=m+2\Leftrightarrow mx+x+mx-m=m+2\Leftrightarrow2mx+x=2m+2\Leftrightarrow\left(2m+1\right)x=2m+2\) ,để hpt có nghiệm duy nhất thì \(2m+1\ne0\Leftrightarrow m\ne-\frac{1}{2}\). Hệ pt có nghiệm duy nhất khi \(m\ne-\frac{1}{2}\) là:\(\left\{{}\begin{matrix}x=\frac{2m+2}{2m+1}\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1+\frac{1}{2m+1}\\y=\frac{1}{2m+1}\end{matrix}\right.\) . Để \(x^2+y^2\) nhỏ nhất \(\Leftrightarrow\left(1+\frac{1}{2m+1}\right)^2+\left(\frac{1}{2m+1}\right)^2\) nhỏ nhất
\(\Rightarrow\) tìm gtnn của \(\left(1+\frac{1}{2m+1}\right)^2+\left(\frac{1}{2m+1}\right)^2\)\(\left(1+\frac{1}{2m+1}\right)^2+\left(\frac{1}{2m+1}\right)^2=1+\frac{2}{2m+1}+\left(\frac{1}{2m+1}\right)^2+\left(\frac{1}{2m+1}\right)^2=1+\frac{2}{2m+1}+2\left(\frac{1}{2m+1}\right)^2=2\left[\left(\frac{1}{2m+1}\right)^2+\frac{1}{2m+1}+\frac{1}{4}\right]+\frac{1}{2}=2\left(\frac{1}{2m+1}+\frac{1}{2}\right)^2+\frac{1}{2}\) \(\Rightarrow\left(1+\frac{1}{2m+1}\right)^2+\left(\frac{1}{2m+1}\right)^2\) nhỏ nhất bằng 1/2. Dấu "\(=\)" xảy ra khi \(\frac{1}{2m+1}=-\frac{1}{2}\Leftrightarrow2m+1=-2\Leftrightarrow m=-\frac{3}{2}\left(tman\right)\). Vậy m\(=-\frac{3}{2}\)
sai bạn sửa lại nhé
NH
31 tháng 1 2023
sửa lại nhé
\(\left\{{}\begin{matrix}3\left(x-y\right)-y=11\\x-2\left(x+5y\right)=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)
Y
31 tháng 1 2023
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\left(1\right)\end{matrix}\right.\)
Nhân \(-3\) vào \(\left(1\right)\)
\(\left\{{}\begin{matrix}3x-4y=11\left(2\right)\\3x+30y=45\left(3\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(3\right)\) :
\(\Leftrightarrow3x-3x-4y-30y=11-45\)
\(\Leftrightarrow-34y=-34\)
\(\Leftrightarrow x=1\)
Lấy \(x=1\) thay vào \(\left(2\right)\) : \(3.1-4y=11\Leftrightarrow y=2\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(1;2\right)\)
CB
1
17 tháng 6 2021
a) A = \(13-2\sqrt{42}=\left(\sqrt{7}-\sqrt{6}\right)^2\)
<=> \(\sqrt{A}=\sqrt{7}-\sqrt{6}\)
b) \(A=46+6\sqrt{5}=\left(\sqrt{45}+1\right)^2\)
<=> \(\sqrt{A}=\sqrt{45}+1\)
c) \(A=12-3\sqrt{15}=\dfrac{1}{2}\left(24-6\sqrt{15}\right)=\dfrac{1}{2}\left(\sqrt{15}-3\right)^2\)
<=> \(\sqrt{A}=\dfrac{1}{\sqrt{2}}\left(\sqrt{15}-3\right)\)
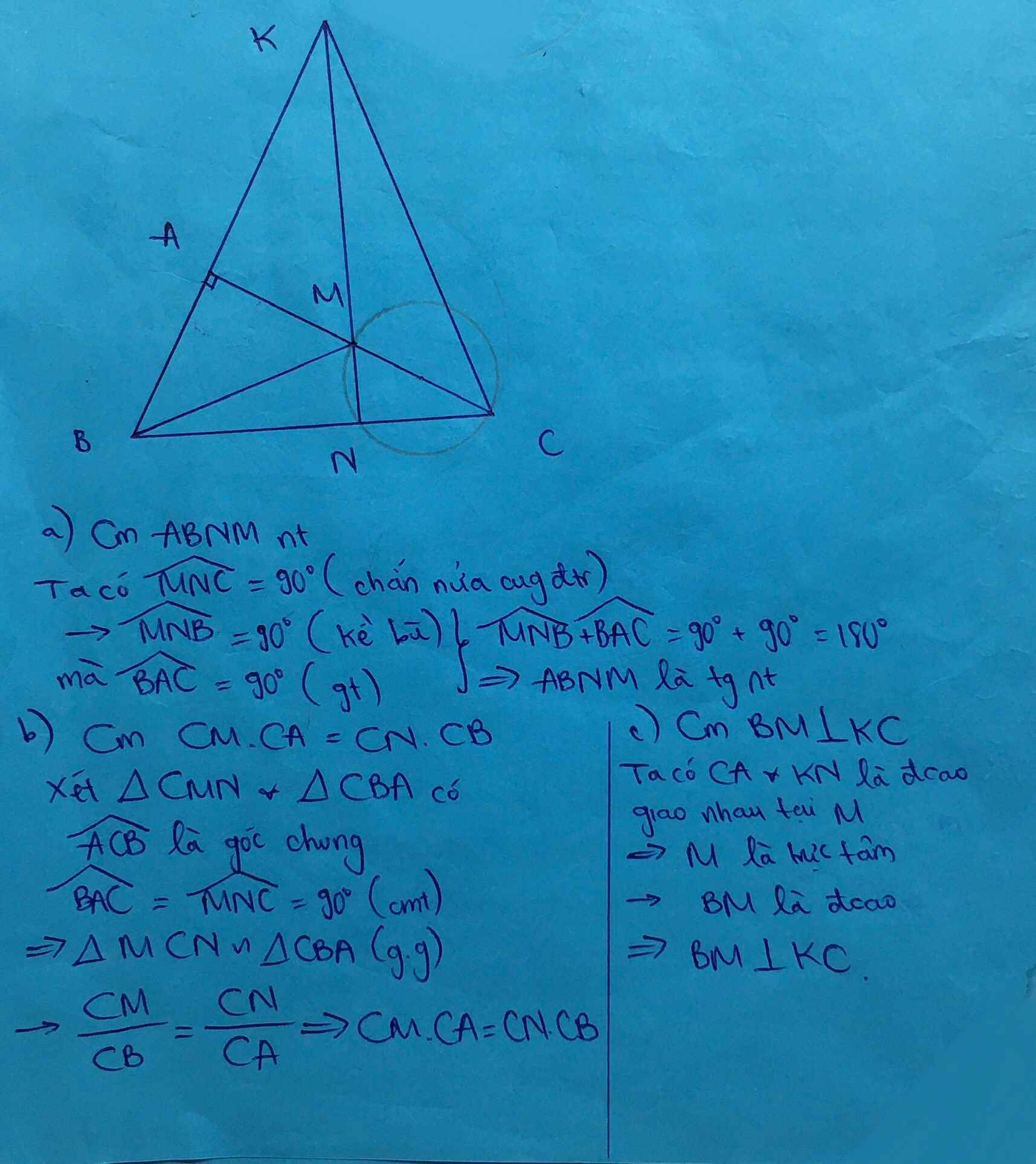
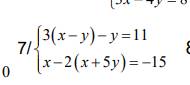
c: Xét ΔHDK vuông tại H và ΔHIB vuông tại H có
góc HDK=góc HIB
=>ΔHDK đồng dạng với ΔHIB
=>HD/HI=HK/HB
=>HD*HB=HI*HK=AH^2