Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3: (SBT/24):
a. \(\dfrac{5x+3}{x-2}\)=\(\dfrac{5x^2+13x+6}{x^2-4}\)
(5x+3) . (x2-4) = 5x3-20x+3x3-12
(x-2) . (5x2+13x+6) = 5x3+13x2+6x-10x2-26x-12 = 5x3-20x+3x2-12
=> (5x+3) (x2-4) = (x-2) (5x2+13x+6)
Vậy \(\dfrac{5x+3}{x-2}\)=\(\dfrac{5x^2+13x+6}{x^2-4}\)(đẳng thức đúng)
b. \(\dfrac{x+1}{x+3}\)=\(\dfrac{x^2+3}{x^2+6x+9}\)
(x+1) . (x2+6x+9) = x3+6x2+9x+x2+6x+9 = x3+7x2+15x+9
(x+3) . (x2+3) = x3+3x+3x2+9
=> (x+1) (x2+6x+9) ≠ (x+3) (x2+3)
Vậy \(\dfrac{x+1}{x+3}\)≠\(\dfrac{x^2+3}{x^2+6x+9}\)(đẳng thức sai)
Chữa lại: \(\dfrac{x+1}{x+3}\)=\(\dfrac{x^2+3}{x^{2_{ }}+6x+9}\)
c. \(\dfrac{x^2-2}{x^2-1}\)=\(\dfrac{x+2}{x+1}\)
(x2-2) . (x+1) = x3+x2-2x-2
(x2-1) . (x+2) = x3+2x2-x-2
=> (x2-2) (x+1) ≠ (x2-1) (x+2)
Vậy \(\dfrac{x^2-2}{x^2-1}\)≠\(\dfrac{x+2}{x+1}\)(đẳng thức sai)
Chữa lại: \(\dfrac{x^2+x-2}{x^2-1}\)=\(\dfrac{x+2}{x+1}\)
d. \(\dfrac{2x^2-5x+3}{x^2+3x-4}\)=\(\dfrac{2x^2-x-3}{x^2+5x+4}\)
(2x2-5x+3) . (x2+5x+4) = 2x4+10x3+8x2-5x3-25x2-20x+3x2+15x+12
= 2x4+5x3-14x2-5x+12
(x2+3x-4) . (2x2-x-3) = 2x4-x3-3x2+6x3-3x2-9x-8x2+4x+12
= 2x4+5x3-14x2-5x+12
=> (2x2-5x+3) (x2+5x+4) = (x2+3x-4) (2x2-x-3)
Vậy \(\dfrac{2x^2-5x+3}{x^2+3x-4}\)=\(\dfrac{2x^2-x-3}{x^2+5x+4}\)

`a,x^3-8 ne 0`
`=>x^3 ne 8`
`=>x ne 2`
`b,2x^2+5x+3 ne 0`
`=>2x^2+2x+3x+3 ne 0`
`=>2x(x+1)+3(x+1) ne 0`
`=>(x+1)(2x+3) ne 0`
`=>x ne -1,-3/2`
`c,x^2-4 ne 0`
`=>x^2 ne 4`
`=>x ne 2,-2`
a) ĐK:
\(x^3-8\ne0\\ \Leftrightarrow x\ne2\)
b) ĐK:
\(2x^2+5x+3\ne0\\ \Leftrightarrow\left[{}\begin{matrix}x\ne-1\\x\ne-\dfrac{3}{2}\end{matrix}\right.\)
c) ĐK:
\(x^2-4\ne0\\ \Leftrightarrow x\ne\pm2\)
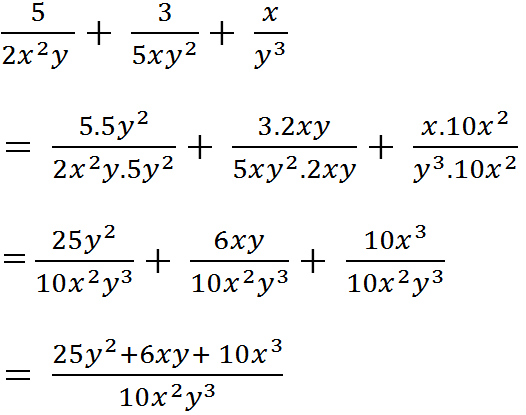



\(=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)