ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
HT
Huyền Trân
15 tháng 9 2019 - olm

Cộng các phân thức

a ) 1/( x-y)(y-z) + 1/ ( y-z)(z-x) + 1/ (z-x)(x-y) b ) 4/(y-x)(z-x) + 3/(y-x)(y-z)+ 3/(y-x)(x-z)
#Toán lớp 8
1
KS
Kudo Shinichi
15 tháng 9 2019

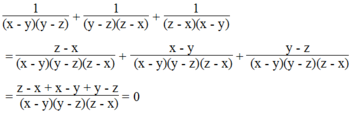
a ) \(\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}\)

     = \(\frac{z-x}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{x-y}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\)

    = \(\frac{z-x+x-y+y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=0\)

b ) \(\frac{4}{\left(y-x\right)\left(z-x\right)}+\frac{3}{\left(y-x\right)\left(y-z\right)}+\frac{3}{\left(y-z\right)\left(x-z\right)}\)

 = \(\frac{-4}{\left(y-x\right)\left(x-z\right)}+\frac{3}{\left(y-x\right)\left(y-z\right)}+\frac{3}{\left(y-z\right)\left(x-z\right)}\)

= \(\frac{-4\left(y-z\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}+\frac{3\left(x-z\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}+\frac{3\left(y-x\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}\)

= \(\frac{-4y+4z+3x-3z+3y-3x}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}=\frac{z-y}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}\)

= \(\frac{-\left(y-x\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}=\frac{-1}{\left(x-z\right)\left(y-z\right)}=\frac{1}{\left(x-z\right)\left(x-y\right)}\)

Chúc bạn học tốt !!!

Đúng(1)
NN
Nguyễn Ngọc Phượng
7 tháng 7 2016

Cộng các phân thức đại số :

  \(\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}\)
#Toán lớp 8
1
VD
Võ Đông Anh Tuấn
7 tháng 7 2016

\(\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}\)

\(=\frac{z-x+x-y+y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\)

\(=0\)

Đúng(0)
NN
Nguyễn Ngọc Phượng
7 tháng 7 2016

giỏi quá . Cho hỏi anh học lớp mấy

Đúng(0)
SG
Sách Giáo Khoa
28 tháng 4 2017
Cộng các phân thức : a) \(\dfrac{1}{\left(x-y\right)\left(y-z\right)}+\dfrac{1}{\left(y-z\right)\left(z-x\right)}+\dfrac{1}{\left(z-x\right)\left(x-y\right)}\) b)...
Đọc tiếp

Cộng các phân thức :

a) \(\dfrac{1}{\left(x-y\right)\left(y-z\right)}+\dfrac{1}{\left(y-z\right)\left(z-x\right)}+\dfrac{1}{\left(z-x\right)\left(x-y\right)}\)

b) \(\dfrac{4}{\left(y-x\right)\left(z-x\right)}+\dfrac{3}{\left(y-x\right)\left(y-z\right)}+\dfrac{3}{\left(y-z\right)\left(x-z\right)}\) 

c) \(\dfrac{1}{x\left(x-y\right)\left(x-z\right)}+\dfrac{1}{y\left(y-z\right)\left(y-x\right)}+\dfrac{1}{z\left(z-x\right)\left(z-y\right)}\)
#Toán lớp 8
1
NT
Nguyen Thuy Hoa
28 tháng 6 2017

Phép cộng các phân thức đại số

Phép cộng các phân thức đại số

Đúng(0)
KT
Kiều Trung Hiếu
13 tháng 12 2017 - olm

Cộng các pthuc

1/x(x-y)(x-z) + 1/y(y-z)(y-x) + 1/z(z-x)(z-y)

M.n chịu khó đọc nhé cả viết phân số ở olm máy mình bị lỗi 
#Toán lớp 8
0
TL
Trần Lưu Duyên Hạ
27 tháng 11 2019 - olm

cộng phân thức: M = 2/x-y + 2/y-z+2/z-x+{[(x-y)^2 + (y-z)^2 + (z-x)^2]/(x-y)(y-z)(z-x)}
#Toán lớp 8
0
AX
asuna x kirito
18 tháng 10 2015 - olm

1/x(x-y)(x-z)+1/y(y-z)(y-x)+1/z(z-x)(z-y)

tính tổng của phân thức 
#Toán lớp 8
0
TT
ta thi hong hai Tathpthunghoa
13 tháng 11 2019 - olm

Cộng các phân thức đại số sau vào với nhau:

\(\frac{1}{\left(y-z\right)\left(x^2+xz-y^2-yz\right)}+\frac{1}{\left(z-x\right)\left(y^2+xy-z^2-zx\right)}+\frac{1}{\left(x-y\right)\left(z^2+yz-x^2-xy\right)}\)
#Toán lớp 8
1
TT
ta thi hong hai Tathpthunghoa
13 tháng 11 2019

Giúp mình với các bạn

Đúng(0)
NT
Nguyễn Thị Thanh Bình
17 tháng 8 2020 - olm

Phân tích đa thức thành nhân tử

d (a² + a)² + 4(a² + a) - 12

e) (x² + x + 1)( x² + x + 2) -12

g) x⁸ + x + 1 h) x¹⁰ + x⁵ + 1

i) x³ ( z -y² ) + y³ ( x - z² ) + z³ ( y - x² ) + xyz( xyz - 1 )

k) x(y - z)² + y(z - x)² + z(x - y)² - x³ - y³ - z³ + 4xyz

l) (x + y + z)³ - (x + y - z)³ - (y + z - x)³ - (z + x - y)³
#Toán lớp 8
2
NT
Nguyễn Thị Thanh Bình
17 tháng 8 2020

mọi người ơi giúp mk nhanh nha cần ngay bây giờ

Đúng(0)
NN
Nobi Nobita
17 tháng 8 2020

d) \(\left(a^2+a\right)^2+4\left(a^2+a\right)-12=\left(a^2+a\right)^2+4\left(a^2+a\right)+16-4\)

\(=\left(a^2+a+2\right)^2-4=\left(a^2+a+2-4\right)\left(a^2+a+2+4\right)\)

\(=\left(a^2+a-2\right)\left(a^2+a+6\right)=\left(a-1\right)\left(a+2\right)\left(a^2+a+6\right)\)

Đúng(0)
KT
Kim Tae Huynh 123
2 tháng 5 2019 - olm

Cho các số thực x,y,z khác nhau thỏa mãn : 

(x-y) : (z-x)(z-y) + (y-z) : (x-y)(x-z) + (z-x) : (y-z)(y-x) = 2014 

tính giá trị của biểu thức P= 1: (x-y) + 1:(y-z) + 1:(z-x)

 
#Toán lớp 8
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP