Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ∆ l 0 là độ biến dạng của lò xo tại vị trí cân bằng
Ta có
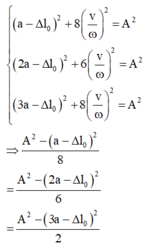
+ Theo tính chất của dãy tỉ số bằng nhau, ta có:
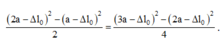
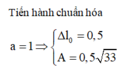
+ Tỉ số giữa thời gian nén và giãn trong một chu kì
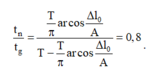
Đáp án A

Chọn chiều dương hướng xuống, gốc O tại VTCB. Gọi a là độ dãn của lò xo khi vật cân bằng, li độ của vật khi lò xo dãn ∆ l là ∆ l -a (cm); ω là tần số góc và A là biên độ của vật.
Ta có hệ:
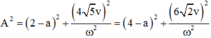
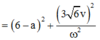
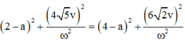
![]()
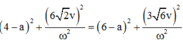
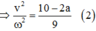
Giải hệ (1) và (2) ta tìm được
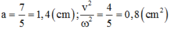
Từ đó tính được A = 8,022 cm.
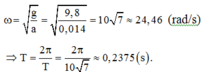
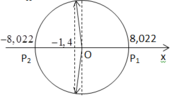
Thời gian lò xo dãn trong một chu kì ứng với vật chuyển động giữa hai li độ -1,4 cm và 8,022cm. Ta chỉ cần tính tốc độ trung bình khi vật đi từ điểm có li độ -1,4 cm đến biên có li độ 8,022 cm với thời gian chuyển động t= T 4 + T 2 π . a r c sin ( a A ) = 0 , 066 ( s )
và quãng đường s = A + a = 9,422 (cm).
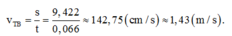

Đáp án A
+ Độ biến dạng của lò xo :![]()
Do vật dao động điều hòa nên phương trình dao động của vật có dạng :![]()
Với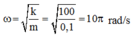
+ Theo bài ra tại t= 0 ![]()
![]()
![]()
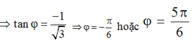
![]()
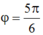
Thay vào (1) ta tìm được : A = 4 cm
![]()
Quảng đường vật đi được trong 1/3 chu kì kể từ thời điểm t = 0 là:
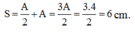

Đáp án A
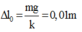
Ta có: ![]()
Quảng đường vật đi được trong một phần ba chu kì kể từ thời điểm ban đầu t= 0 là :
![]()

ĐĐáp án C
+ Gọi x1, x2, x3 là li độ ứng với từng vị trí giãn của lò xo.
AÁp dụng công thức độc lập ta được:

Lấy (2) - (1) và (3) - (1) ta được:
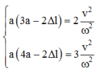
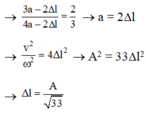
+ Thời gian lò xo nén tương ứng với vật dao động từ vị trí có ly độ Dl đến ly độ -A ứng với góc quét là:
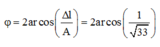
® Thời gian nén là:
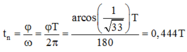
+ Thời gian lò xo giãn là:
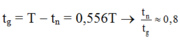

+ Ta có: Δ l = m g k = 1 cm
® Vị trí lò xo dãn 3 cm có: x = 2 cm
+ ω = k m = 10 10 rad/s
+ Áp dụng công thức độc lập ta được:
A = x 2 + v 2 ω 2 = 2 2 + 20 π 3 2 10 10 2 = 4 cm
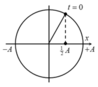
+ Dựa vào đường tròn ta xác định được vị trí t = 0
+ Từ t = 0 đi trong T 3 tương ứng với góc quét là φ = ω t = 2 π T . T 3 = 2 π 3
Tương ứng trên đường tròn là đi tới điểm A.
® S = A + A 2 = 6 cm
ĐÁP ÁN A


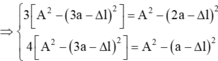
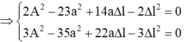
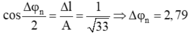
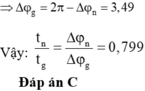

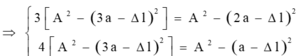
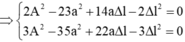
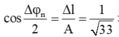
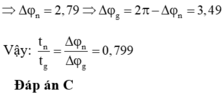
Đáp án B
+ Gọi ∆ 0 là độ biến dạng của lò xo tại vị trí cân bằng
Ta có
+ Ta tiến hành chuẩn hóa
Thời gian lò xo bị nén ứng với góc α , với
→ Tỉ số thời gian lò xo bị nén và bị giãn